Álgebra lineal
El campo de las matemáticas es sumamente extenso y se divide en varias ramas para un mejor estudio. El álgebra es una de esas ramas la cual utiliza una serie de números, signos y letras con el objetivo de poder hacer referencia a diferentes o múltiples operaciones aritméticas. También existen varios tipos de álgebra y entre ellos encontramos el álgebra lineal la cual se encarga de estudiar ecuaciones lineales.
¿Qué es el álgebra lineal?
El álgebra lineal es una de las ramas que forman parte de la matemática que se encarga de realizar estudios relacionados con vectores, matrices, espacios duales y sistemas relacionados con ecuaciones lineales para analizar los espacios vectoriales y sus transformaciones.
Definición
El álgebra lineal es una rama de la matemática que se encarga de estudiar a los conjuntos conocidos con el nombre de espacios vectoriales y las transformaciones lineales las cuales son funciones que se dan entre espacios vectoriales dentro de las condiciones de linealidad. Es una ciencia que puede llegar a resolver diferentes tipos de operaciones aritméticas por medio del uso de signos, letras y números.
Características del álgebra lineal
Entre las principales características que se presentan en el álgebra lineal encontramos:
- Utiliza una serie de letras y símbolos para sustituir los números y de esta forma representar los procedimientos o las operaciones aritméticas.
- Estudia estructuras matemáticas en las cuales se pueden realizar sumas entre diferentes elementos de un mismo conjunto o también para multiplicar los elementos por números reales o complejos.
- Los signos, letras y números que utiliza son los responsables de representar entidades numéricas las cuales se conocen con el nombre de variables.
- La palabra lineal, hace referencia a fuente vinculado a una línea determinada o raya de sucesión.
- Estudia aspectos relacionados con vectores y sus espacios, matrices y ecuaciones de tipo lineal.
Historia
Las primeras culturas que lograron resolver ecuaciones del tipo lineal y cuadráticas fueron los egipcios y los babilonios, de hecho, esta última cultura utilizaba prácticamente los mismos métodos que se usan en la actualidad para resolver a situaciones de tipo cuadráticas. Los primeros sistemas de ecuaciones lineales más elaborados y estructurados tuvieron su origen en Europa alrededor del año 1637 gracias a las contribuciones hechas por René Descartes a las coordenadas en el campo de la geometría.
El álgebra lineal creció con el paso del tiempo y con varias definiciones nuevas que se fueron agregando a su paso. Arthur Cayley fue quien se encargó de introducir la multiplicación del tipo matricial y la matriz inversa en el año 1856. Este trabajo fue ampliado de forma importante gracias a Benjamin Peirce y Charles Sanders Peirce. Una definición más moderna sobre el tema se realizó en el año 1888 gracias a Peano ya para el siglo XX, la definición y el concepto de álgebra lineal había tomado una forma más moderna.
Para qué sirve el álgebra lineal
El álgebra lineal es un instrumento muy utilizado en la actualidad sobre todo en el campo de la matemática moderna, en la física, computación e ingeniería. Es una ciencia que sirve para poder analizar y estudiar las diferentes bases teóricas y prácticas relacionadas con vectores, cálculo de raíces, sistemas de ecuaciones lineales, espacios vectoriales y sus transformaciones. En el campo de la Ingeniería Industrial es utilizada principalmente en el campo de la estadística y se encuentra también relacionada con algunas áreas no matemáticas como por ejemplo el análisis funcional, las ecuaciones diferenciales y los gráficos por computadora.
Elementos
Los elementos del álgebra lineal son los siguientes:
- Vectores: los vectores son un tipo de trazado de uno o varios elementos de la recta los cuales sugieren una dirección proyectada en un determinado espacio, son líneas que poseen una magnitud, dirección y sentido concreto. Se representan de forma gráfica como segmentos rectilíneos y se componen por dirección, orientación, origen y longitud o módulo.
- Matriz: la materia es un conjunto bidimensional de números o de elementos los cuales se encuentran colocados en filas y columnas organizadas de forma rectangular. La matriz hace posible una representación de los coeficientes de las ecuaciones lineales.
- Raíz: es la cantidad que se multiplica por sí misma las veces que sea indicado para lograr de esta manera obtener una cantidad como resultado. Es un proceso que consiste en hallar la base de la potencia cuando se conoce el exponente de la raíz y la cantidad que pertenece al sub radical.
- Determinante: es un tipo de expresión que puede ser obtenida por medio de la aplicación de los elementos que forman parte de la matriz cuadrada.
Importancia
El álgebra lineal resulta ser un tipo de matemática fundamental para varias aplicaciones y campos de estudio, como por ejemplo la física, la arquitectura y la ingeniería. Pero sus aplicaciones incluso van más allá de esto pues también es necesaria para realizar estudios arqueológicos, análisis de tráfico y es un componente fundamental de las redes de comunicación. Es importante porque brinda la capacidad para poder resolver una gran cantidad de problemáticas por medio de herramientas lógicas y matemáticas con los cuáles pueden ser desarrollados diferentes situaciones que se presentan en la vida cotidiana.
Ejemplos de álgebra lineal
Un ejemplo de transformación lineal es:
![]()
El operador derivada satisface las condiciones de linealidad, y se ilustra la primera condición de linealidad:
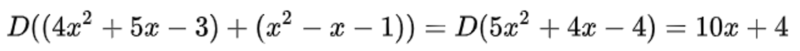
¿Cómo citar este artículo?
Briceño V., Gabriela. (2021). Álgebra lineal. Recuperado el 2 enero, 2025, de Euston96: https://www.euston96.com/algebra-lineal/