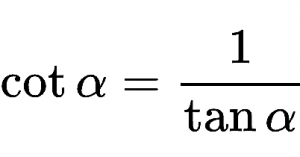Ángulo agudo

El área de las matemáticas es un campo sumamente extenso y por eso, es común encontrar una gran cantidad de conceptos. Uno de ellos es el ángulo, una porción de un plano que se encuentra comprendida en medio de dos semirrectas y que además tiene un origen el cual se conoce con nombre de vértice. Existen además, muchos tipos de ángulos, en este caso se explicará el ángulo agudo.

Temas relacionados

Ángulos adyacentes, ángulos complementarios, ángulos consecutivos, ángulos correspondientes, ángulo llano, ángulos suplementarios, ángulo obtuso, ángulos congruentes

¿Qué es un ángulo agudo?

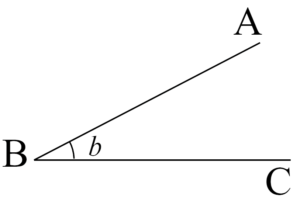
El ángulo agudo es el tipo de ángulo que se encuentra ubicado entre dos rectas las cuales se caracterizan por tener un mismo vértice y que además tiene una inclinación mayor a 0 y menor que 0.

Definición

Este tipo de ángulo es en realidad bastante común y lo podemos encontrar en muchos tipos de figuras geométricas como rombos, triángulos, cuadriláteros y muchas más. Su nombre proviene del idioma griego, de la palabra “ankulos”, la cual significa “doblado”. Por otro lado, la palabra agudo proviene del idioma latín, de la palabra “acutus” la cual tiene como significado “agudo”.

Entonces, se puede definir al ángulo agudo como el tipo de ángulo que tiene o que está formado por dos rectas las cuales tienen cada una el mismo vértice y que además cuentan con una amplitud mayor a O grados pero al mismo tiempo menor a 90 grados (amplitud > 0° y < 90°).

Características

Las principales características que pueden ser encontradas en los ángulos agudos se mencionan a continuación:

• Son ángulos que se caracterizan por tener una amplitud superior a los 0°.
• Son considerados como los ángulos de menor tamaño en el mundo de las matemáticas.
• Se encuentra localizado entre dos rectas las cuales comparten el mismo vértice.
• Para poder medirlos se puede utilizar un aparato conocido como transportador.
• Puede ser encontrado en algunos triángulos y en figuras geométricas
• Se encuentran dentro del grupo de ángulos conocidos como convexos.

Cuánto mide un ángulo agudo

El ángulo agudo tiene una medida que se ubica entre los 0° y los 90°. Si se consideraran únicamente los números enteros que conforman la medida de los ángulos agudos podríamos decir que miden entre 1° y 89°. Otro aspecto importante en cuanto a su medida en la forma en la que estos ángulos pueden ser medidos, para ello es necesario utilizar un transportador el cual es un instrumento de medición matemático que puede tener dos formar, una semicircular y otra circular, éste último se utiliza para medir ángulos que pueden llegar a medir hasta 400°.

Funciones trigonométricas de un ángulo agudo

Las funciones trigonométricas que posee un ángulo agudo son definidas en la función que tienen los lados del triángulo y cada una de ellas son independientes del tamaño que el triángulo tenga. Las funciones trigonométricas son las siguientes:

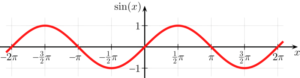
Seno

El seno de un triángulo agudo es igual al cociente que existe entre la longitud del cateto opuesto (c) y el ángulo y la longitud que tiene la hipotenusa (a). Puede ser representado como: sen(α) o sin(α). Además, su fórmula es la siguiente:

sin(α)= cateto opuesto / hipotenusa = c / a

Coseno

El coseno que tiene un ángulo agudo es igual al cociente que existe entre la longitud del cateto continuo (b) con respecto al ángulo y la longitud que tiene la hipotenusa (a). El coseno puede ser representado como cos(α) y su fórmula es la siguiente:

cos(α)= cateto contiguo / hipotenusa = b / a

Tangente

La tangente de un ángulo agudo es igual al cociente que existe entre la longitud que tiene el cateto opuesto al ángulo (c) y la longitud que tiene el cateto opuesto (b). Es representada como tg (α) o tan(α) y su fórmula es la siguiente:

tg(α)= cateto opuesto / cateto contiguo = c / b

Cosecante

La cosecante se refiere a la relación de tipo inversa del seno, en otras palabras, el cociente entre la longitud que tiene la hipotenusa (a) y la longitud que tiene el cateto opuesto al ángulo (c). Es representado como cosec(α) o csc(α). Su fórmula es la siguiente:

csc(α)= 1 / sin(α) = hipotenusa / cateto opuesto = a / c

Secante

La secante del triángulo agudo es la relación inversa que se da en el coseno, en otras palabras, el cociente entre la longitud que tiene la hipotenusa y la longitud que posee el cateto contiguo al ángulo (b). Es representado como sec(α). Su fórmula es la siguiente:

sec(α)= 1 / cos(α) = hipotenusa / cateto contiguo = a / b

Cotangente

La cotangente del ángulo agudo es igual al cociente entre la longitud del cateto contiguo del ángulo (c) y la longitud que tiene el cateto opuesto (b). Es representado como cotg(α) o cot(α) y su fórmula se menciona a continuación:

cot(α)= 1 / tg(α) = cateto contiguo / cateto opuseto = b / c

Qué objetos forman un ángulo agudo

Es común encontrar este tipo de ángulo incluso en la vida cotidiana, algunos ejemplos son:

• El ángulo que se forma en una escalera de dos piezas, entre el lado del soporte y el lado por donde se asciende, este espacio representa un ángulo agudo.
• En una tijera, sus navajas están dispuestas de manera tal que cuando se abren forman un ángulo agudo el cual de hecho se va encogiendo hasta que la escalera cierra por completo.
• Cuando escribimos, el lápiz y la mano forman un ángulo agudo. Si se colocara el lápiz de forma más elevada, entonces observaríamos como la escritura se vuelve más complicada.
• Cuando se practica la pesca, la caña se coloca en un ángulo agudo para que de esta forma se pueda aprovechar la mayor cantidad de fuerza para atrapar el pez.

Ejemplos

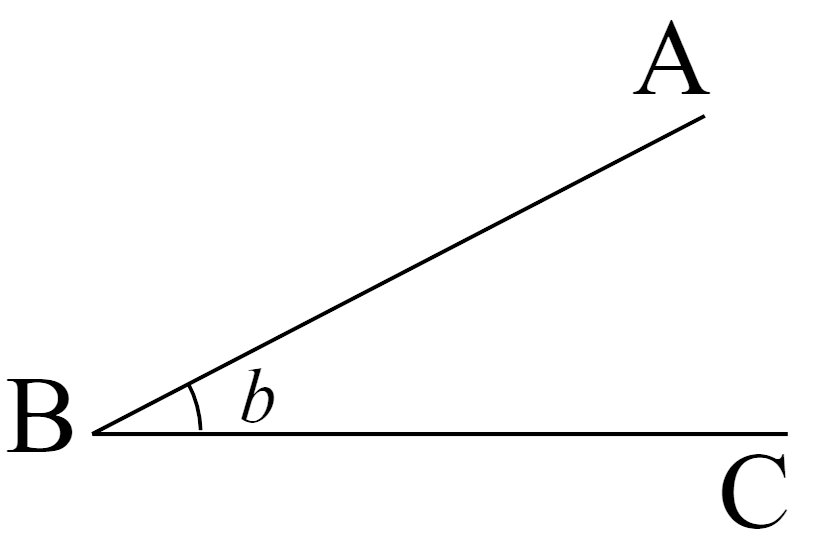
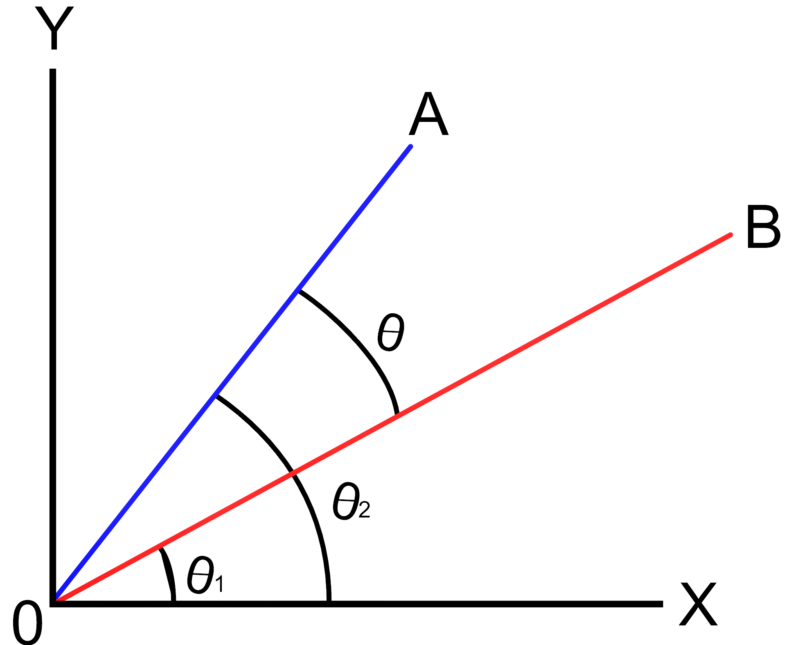
A continuación se muestran y mencionan algunos tipos de ángulos agudos que podemos encontrar: