Ángulos complementarios

La palabra ángulo, que procede del vocablo latino angŭlus, se refiere a una figura matemática dentro del área de la geometría que se forma a partir de dos rectas cuando éstas se cortan entre sí en una misma superficie. El ángulo entonces es la región del plano que está comprendida entre dos semirrectas o lados que poseen el mismo origen o vértice. Estos ángulos pueden llegar a ser medidos en unidades específicas y con diferentes medidas como resultado y dependiendo de ellas, reciben una determinada clasificación, y es importante aclarar que la medida de los ángulos siempre será hecha en grados.

Temas relacionados

Ángulos adyacentes, ángulo agudo, ángulos consecutivos, ángulos correspondientes, ángulo llano, ángulos rectos, ángulos suplementarios, ángulo obtuso, ángulos congruentes

¿Qué son ángulos complementarios?

Los ángulos complementarios son el tipo de ángulo que cuando se suman dan un total de 90 grados. Cuando los ángulos son complementarios tienen la medida que tienen los ángulos rectos.

Definición

Para poder conocer y entender el significado del término ángulos complementarios, debemos primero conocer el origen etimológico de las palabras que la forman. La palabra ángulo es de origen griego, la cual deriva de la palabra “ankulos”, que significa “torcido”. Luego se difundió al latín en forma de “angulus” con el significado de “ángulo”.

Por otro lado, la palabra complementario, es de procedencia latina. Nace de la suma de varias partes muy bien diferenciadas: el prefijo “com-”, que significa “unión”; el verbo “plere”, que es sinónimo de “llenar”; “-mento”, que puede definirse como “medio”, y, por último, el sufijo “-ario”. Este último se utiliza para indicar “relativo a”.

Dicho esto, es importante recordar también que los ángulos tienen diferentes medidas y que dependiendo de ellas, los ángulos reciben su nombre y clasificación, de esta forma, podemos decir que, los ángulos complementarios son aquellos ángulos que juntos suman 90 grados (90º).

Características

Las principales características de los ángulos complementarios son las siguientes:

• Sean o no consecutivos siempre sumarán matemáticamente 90 grados.
• Puede ser que los ángulos no estén juntos pero si entre dos ángulos logran hacer la suma de 90 grados, entonces serán complementarios.
• Cuando dos ángulos suman 90 grados, entonces se considera que esos ángulos se complementan.
• Son ángulos que suman la medida que tiene un ángulo recto.
• Los ángulos complementarios también están compuestos por dos lados y por un vértice en el origen cada uno.
• Es importante conocer los ángulos complementarios porque los podemos encontrar en muchas formas en la naturaleza y en muchos fenómenos físicos.
• Pueden ser utilizados en la arquitectura, en la construcción, en la fisionomía, etc.
• Dos ángulos no necesitan ser adyacentes para ser complementarios.

Cómo hallar ángulos complementarios

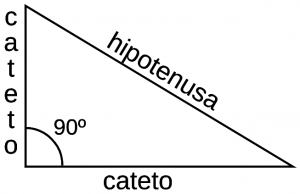
Recordando que los ángulos complementarios son aquellos que cuando se suman dan como resultado 90 grados o π/2 rad. Suponiendo que tenemos dos ángulos: α = 50⁰ y β = 40⁰, si los sumamos nos dará como resultado 90°, por lo tanto, decimos que los ángulos se complementan. Por ejemplo, en un triángulo rectángulo, la suma de los ángulos internos es igual a 180°, lo tanto, decimos que en el triángulo rectángulo los ángulos agudos se consideran complementarios.

Funciones trigonométricas de los ángulos complementarios

Las funciones trigonométricas son funciones que han sido establecidas con el propósito de ampliar las razones de los números reales y complejos. Estas funciones son muy importantes en diversas áreas como la física, astronomía, cartografía y telecomunicaciones. Por lo general se definen como el cociente que existe entre los lados de un triángulo rectángulo y su relación con los ángulos. En el caso de los ángulos complementarios, sea β el ángulo complementario de α, siendo β = 90º – α, las razones trigonométricas del ángulo complementario pueden ser obtenidas en función de las razones trigonométricas de α.

Las razones trigonométricas de los ángulos complementarios son entonces las siguientes:

• Seno del ángulo complementario:

sen (90° – α) = cos α

• Coseno del ángulo complementario:

cos (90° – α) = sen α

• Tangente del ángulo complementario:

Tan (90° – α) = cot α

• Cosecante del ángulo complementario:

csc (90° – α) = sec α

• Secante del ángulo complementario:

sec (90° – α) = csc α

• Cotangente del ángulo complementario:

cot (90° – α) = tan α

Ejemplos

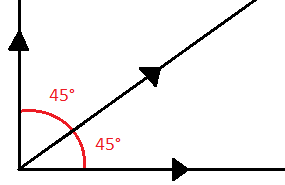
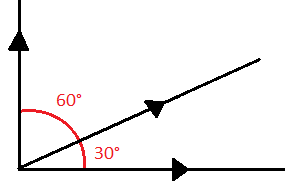
Algunos ejemplos de ángulos complementarios son los siguientes: