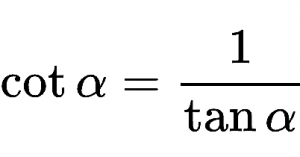Ángulos suplementarios

Los ángulos suplementarios son el tipo de ángulo en el que entre sus ángulos lograr sumar 180 grados haciéndolos diferentes de los ángulos complementarios que únicamente forman 90 grados. Siguiendo la propiedad y fórmula de los ángulos que se complementan entre sí, cuando un ángulo tiene menos de 180 grados le corresponderá entonces un ángulo que lo suplemente según la fórmula A (ángulo suplementario) = 180° menos (-) el ángulo que necesita suplemento. Ejemplo: A = 180° – 150° = 30°. El suplementario de un ángulo de 45° es otro de 135°. El suplementario de un ángulo de 179° sería entonces un ángulo de 1° y el suplementario de un ángulo que mida 90° es otro de la misma medida.

Temas relacionados

Ángulos adyacentes, ángulo agudo, ángulos complementarios, ángulos consecutivos, ángulos correspondientes, ángulo llano, ángulos rectos, ángulo obtuso, ángulos congruentes

¿Qué es un ángulo suplementario?

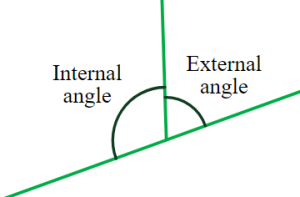
Definimos como ángulos suplementarios a aquellos ángulos cuyas medidas conjuntas logran alcanzar los 180°. Es importante mencionar que dos ángulos no tienen que ser adyacentes para ser suplementarios.

Definición

Los ángulos suplementarios son los ángulos que cuando se suman, logran alcanzar una cifra de 180° de manera que el ángulo A y el ángulo B suman un total de 180°.

La aplicación que tienen los ángulos suplementarios en la práctica o en la vida diaria es muy técnica, es especial para realizar el cálculo de los ángulos arquitectónicos y es de mucha importancia en la construcción, porque cuando segmenta una circunferencia se logra crear una línea de diámetro y dividirla en cualquier punto obteniendo, para de esta manera lograr obtener un ángulo con su suplementario.

Los ángulos suplementarios los podemos ver reflejados en nuestra vida cotidiana, por ejemplo, en las manillas de un reloj que constantemente crea diferentes ángulos complementarios. Los ángulos suplementarios son comunes también en aquellas estructuras que deben de soportar grandes pesos, como por ejemplo la carpa de un circo, la cual debe de encontrarse fijada al piso o a una superficie plana, y la cuerda debe estar atada a la estaca forma un ángulo, que suplementa el espacio restante hasta el suelo. En puentes de arco también se pueden apreciar ángulos suplementarios en las bases, al igual, forman un ángulo que se suplementa con el otro formado en el vacío. Una viga perpendicular al suelo puede formar dos ángulos complementarios entre sí.

Cómo se obtienen los ángulos suplementarios

Para lograr obtener el ángulo suplementario β de un determinado ángulo α, se debe de realizar una resta, de manera que:

Β = 180° – α

Características

Las principales características de los ángulos suplementarios son las siguientes:

• Si dos ángulos suman 180°, entonces decimos que se suplementan.
• Son ángulos que cuando se suman entre sí, dan como resultado dos ángulos rectos.
• Se debe recordar que los ángulos complementarios son equivalentes a un ángulo recto.
• Los podemos encontrar en estructuras de todo tipo, pero principalmente en las que deben de soportar mucho peso.
• Cuando dos ángulos son suplementarios de otros dos ángulos que son congruentes o que tienen la misma medida, entonces los ángulos suplementarios también son congruentes entre sí.
• Los senos de los ángulos suplementarios son los mismos.
• Los cosenos de los ángulos suplementarios son de igual valor absoluto, pero de signo inverso.

Razones trigonométricas de los ángulos suplementarios

Las razones trigonométricas de los ángulos son las siguientes:

• Seno del ángulo suplementario: sen (180° – α) = sen α
• Coseno del ángulo suplementario: cos (180° – α) = -cos α
• Tangente del ángulo suplementario: tan (180° – α) = tan α
• Cosecante del ángulo suplementario: csc (180° – α) = csc α
• Secante del ángulo suplementario: sec (180° – α = -sec α
• Cotangente del ángulo suplementario: cot (180° – α) = -cot α

Ejemplos

Recordemos para poder dar ejemplos que los ángulos suplementarios deben de sumar un total de 180°. Por ejemplo, si tenemos dos ángulos que miden 140 ° y 40 ° respectivamente, sabemos que éstos son ángulos suplementarios, ya que la totalidad de la suma de sus ángulos es igual a 180 °, entonces podemos decir que los siguientes son ejemplos de ángulos suplementarios:

• ¿Cuál es el ángulo suplementario de un ángulo de 60 grados? Un ángulo de 120 grados.
• ¿Cuál es el ángulo suplementario de un ángulo de 20 grados? Un ángulo de 160 grados.