Bisectriz

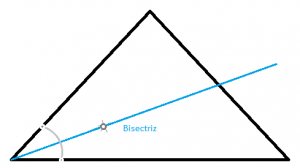
Conocemos con el nombre de bisectriz de un triángulo al segmento que, dividiendo uno de sus tres ángulos en dos partes iguales, termina en el correspondiente lado opuesto. Existen tres bisectrices (Ba, Bb y Bc), según el ángulo en el que empieza.

Temas relacionados

Mediatriz

¿Qué es la bisectriz?

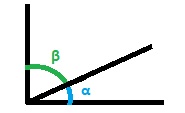
La bisectriz de un ángulo es la semirrecta que tiene su origen en el vértice del ángulo dividiéndolo en dos ángulos que tienen igual medida. Es el lugar geométrico de los puntos del plano de las semirrectas de un ángulo.

Definición

La bisectriz es un término que se utiliza en el área de la geometría y como definición podemos decir que es una recta que al pasar por un ángulo lo logra dividir en dos partes totalmente iguales. Si hablamos desde el punto de vista de la geometría, los puntos que tiene una bisectriz son paralelos, esto quiere decir que tienen la misma distancia en las semirrectas de un ángulo.

Es importante destacar, que se conoce con el nombre de lugar geométrico al grupo de puntos que se encuentran colocados a un lado del punto fijo que posee la recta, ésta tiene un punto de origen y como todas las rectas se expande hasta el infinito, o sea, no tiene final. De la misma manera el punto de la bisectriz tendrá la misma distancia que tienen las dos rectas del ángulo, debido a su correlación. Cuando dos rectas se enlazan dan origen a cuatro ángulos, y cada uno de estos ángulos tiene la función de determinar una bisectriz.

Características

Las principales características de una bisectriz son las siguientes:

• Todos los puntos que posee una bisectriz son paralelos y por esta razón tienen una distancia idéntica a las de la semirrecta en un ángulo.

Propiedades

Al igual que muchas figuras geométricas, la bisectriz también posee propiedades que la diferencias de otros, entre ellas podemos mencionar que:

• Los puntos de la bisectriz se consideran como equidistantes a los dos lados que tiene el ángulo.
• Dos rectas, cuando se intersecan, determinan cuatro ángulos de forma consecutiva y sus bisectrices, que pasan por el punto de intersección, forman cuatro ángulos rectos que son todos consecutivos.
• La bisectriz de un ángulo, con cada uno de los lados tiene la posibilidad de formar dos ángulos con lado común e iguales, cada uno de ellos es la mitad del original.

Cómo se traza la bisectriz

Para lograr trazar o construir una bisectriz debemos de seguir los siguientes pasos:

• Se debe trazar un ángulo.
• Nominar con las letras A, O y B, los ángulos.
• Utilizando un compás hacemos centro en el vértice 0.
• Trazamos un arco de cualquier radio que es el que cortará los lados a y b.
• Con el compás, hacemos centro en los puntos P y Q y trazamos luego dos arcos que tengan el mismo radio y que luego se cortarán en el punto A.
• Utilizando una regla, trazamos una recta que una al vértice 0 con el punto A, y de esta forma podemos obtener la bisectriz del ángulo.

Bisectriz de un ángulo

La bisectriz de un ángulo es la recta que divide el ángulo en dos partes iguales cuando atraviesa el vértice del mismo. Para lograr dibujar la bisectriz de un ángulo debemos de seguir los siguientes pasos:

• Trazar una circunferencia de cualquier amplitud en el centro del vértice del ángulo.
• Desde los puntos donde se elabora el corte de la circunferencia con los lados del ángulo se deben de trazar dos circunferencias que tengan el mismo radio.
• La recta que pasa por el vértice del ángulo y uno de los puntos de corte de las circunferencias es conocida como la bisectriz del ángulo.

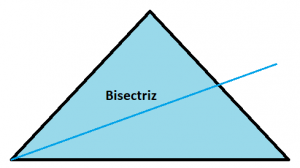
Bisectriz de un triángulo

Podemos definir la bisectriz de un triángulo como el segmento que, dividiendo uno de sus tres ángulos en dos partes iguales, finaliza en el lado opuesto del triángulo. Importante mencionar que existen tres bisectrices que son: Ba, Bb y Bc, dependiendo del ángulo en el que empieza. La longitud de las bisectrices se calculan con la fórmula:

B_a = ( 2/(b+c) )· √( b · c · s (s-a) )

B_b = ( 2/(a+c) )· √( a · c · s (s-b) )

B_c = ( 2/(a+b) )· √( a · b · s (s-c) )

Donde a, b y c son los tres lados del triángulo y s el semiperimetro:

s = (a+b+c) / 2

Las tres bisectrices que tiene un triángulo concurren en un punto que se conoce con el nombre de incentro (I), el cual siempre es un punto interior que existen en cualquier triángulo.

Bisectriz de un segmento

En geometría, se conoce con el nombre de segmento al fragmento de recta que está incluido entre dos puntos, los cuales son llamados puntos extremos o finales. La Bisectriz o bisector de un segmento es entonces una recta o un segmento de recta que pasa por el punto medio de un segmento determinado.

Bisectriz perpendicular

La bisectriz perpendicular es una forma diferente de denominar a la mediatriz, o sea, a la recta que es perpendicular a un segmento y que pasa por su punto medio. Para poder hacer una diferencia de la bisectriz, llamamos entonces a esta bisectriz como angular, aunque también puede ser conocida con el nombre de perpendicular bisectriz. Una bisectriz puede ser una bisectriz perpendicular únicamente si la bisectriz es perpendicular al segmento.

Ejemplos

Algunos ejemplos de bisectrices son los siguientes: