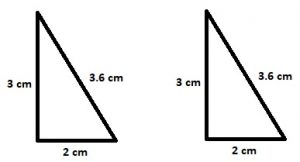
Congruencia de triángulos

En el campo de las matemáticas, dos figuras geométricas pueden ser congruentes cuando éstas figuras tienen las mismas dimensiones y la misma forma sin importar cuál sea su posición u orientación, en otras palabras, si existe una isometría que los relaciona: una transformación que puede ser de traslación, rotación y/o reflexión. Las partes relacionadas entre las figuras congruentes se conocen con el nombre de figuras homólogas o correspondientes.

Temas relacionados

Hipotenusa, triángulo escaleno, triángulo isósceles, triángulo rectángulo

¿Qué es la congruencia de triángulos?

La congruencia de triángulos se da cuando los triangulos tienen la misma forma y también el mismo tamaño y se demuestra que son congruentes cuando sus ángulos correspondientes tienen la misma medida y sus lados son congruentes entre sí.

Definición de congruencia de triángulos

El término congruencia tiene varios significados dependiendo del punto de vista matemático. Por esta razón, dentro del campo de la geometría euclidiana, la congruencia es equivalente a una igualdad matemática la igual que en aritmética y álgebra. En el área de la geometría analítica, la congruencia se define como dos figuras determinadas por puntos que se encuentran sobre un sistema de coordenadas cartesianas las cuales son congruentes entre sí.

En el campo de las matemáticas, dos figuras de puntos pueden ser congruentes cuando tienen los lados iguales y del mismo tamaño si existe una isometría que los relaciona. En otras palabras, dos figuras pueden llegar a ser congruentes si tienen la misma forma y tamaño, sin importar que su posición u orientación sean diferentes. Las partes que coinciden en las figuras congruentes se llaman homólogas o correspondientes.

Formula

En los triángulos semejantes se cumplen las condiciones y fórmulas siguientes:

• Los ángulos homólogos son iguales:

α = α’

β = β’

ϒ = ϒ’

• Los lados homólogos son proporcionales:

a / a’ = b / b’ = c / c’ = r

A r se le denomina razón de semejanza.

Se cumple que la razón de los perímetros de dos triángulos semejantes es también la razón de semejanza y que la razón de sus áreas es el cuadrado de la razón de semejanza:

perímetro / perímetro’ = ( a + b + c ) / ( a’ + b’ + c’ ) = r

área / área’ = r²

Criterios

Los criterios que existen para que se pueda dar la congruencia de los triángulos a menudo son llamados con el nombre de genérica postulados o teoremas de congruencia. Los criterios para que exista una congruencia de triángulos nos dicen que no es necesario verificar la congruencia de los 6 pares de elementos o sea, los 3 pares de lados y 3 pares de ángulos, ya que podemos verificar la congruencia de tres pares de elementos. Estos criterios son los siguientes:

• Dos triángulos son congruentes si dos de sus ángulos son iguales y respectivos al igual que el lado entre ellos. En un triángulo si conocemos dos de sus ángulos el tercer ángulo queda unívocamente determinado.
• Dos triángulos son congruentes si tienen dos lados iguales y el mismo ángulo comprendido entre ellos.
• Dos triángulos son congruentes si tienen los tres lados iguales.
• Dos triángulos son congruentes cuando tienen dos lados y el ángulo sobre uno de ellos de la misma medida. Este caso no es de congruencia si no damos más información sobre el triángulo, como la de ser triángulo rectángulo o si tiene o no ángulos obtusos.

Propiedades de la congruencia de triángulos

Las propiedades que tienen la congruencia de los triángulos son las siguientes:

• Propiedad reflexiva: se aplica en todos los ángulos A y nos dice que un ángulo es congruente a sí mismo.

∢A ≅ ∢A

• Propiedad simétrica: aplica para cualquiera de los ángulos A y B. El orden de la congruencia no tienen ninguna importancia.

Si ∢A ≅ ∢B encontes ∢B ≅ ∢A

• Propiedad transitiva: esta aplica también para cualquiera de los ángulos. Si dos ángulos son congruentes a un tercer ángulo, esto quiere decir que los primeros dos ángulos son congruentes también.

Si ∢A ≅ ∢B y ∢B ≅ ∢C encontes ∢A ≅ ∢C

Aplicación de la congruencia de triángulos

Una forma en la que podemos aplicar el concepto de la congruencia de triángulos en la vida diaria consiste en establecer distancias en la vida cotidiana por lo general cuando usamos un mapa o un diagrama como modelo. Cuando se usan triángulos congruentes para identificar distancias, se deben equiparar los lados de dos triángulos que sean correspondientes.

Otra aplicación importante es la creación de figuras geométricas por medio de construcciones o un dibujo hecho únicamente por medio de una regla y compás y también nos pueden ser útiles en la tarea de encontrar distancias mediante el uso de triángulos congruentes.

Ejemplos

Algunos ejemplos de la congruencia de triángulos son los siguientes:

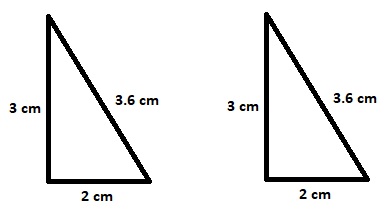
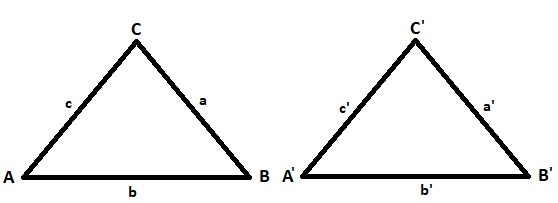
a ≅ a’

b ≅ b’

c ≅ c’