Coseno

El campo de las matemáticas es en realidad muy extenso y en él podemos encontrar una gran cantidad de términos diferentes, todos importantes. Uno de ellos es el coseno, una palabra que está relacionada con las funciones trigonométricas de los triángulos. Estas funciones pueden ser definidas como el cociente que existe entre los dos lados que tiene un triángulo rectángulo el cual está asociado con los ángulos del mismo. A continuación, explicaremos el coseno, una palabra que está también relacionada con la hipotenusa y el cateto.

Temas relacionados

Cosecante, cotangente, seno, teorema del coseno

¿Qué es el coseno?

El término coseno es una palabra que está estrechamente relacionada con el triángulo rectángulo y es una de las partes de las diferentes razones trigonométricas que existen en el campo de las matemáticas.

Definición

El coseno de un triángulo puede ser definido como la razón que existe entre uno de los catetos adyacentes del triángulo que se estudia y su hipotenusa, recordando que ésta es el lado opuesto que se da al ángulo recto que tiene el triángulo rectángulo, en otras palabras, el lado que tiene una mayor longitud, mientras que el cateto será el lado menor.

Características del coseno

Algunas de las principales características del coseno se mencionan a continuación:

• Se representa por medio de la abreviatura cos.
• Es una función trigonométrica.
• Puede ser encontrado en varios tipos de ecuaciones e incluso en las calculadoras en las cuales puede ser fácilmente calculado.
• Es muy utilizado en el campo de la geometría.
• A la relación del coseno se opone siempre el secante.
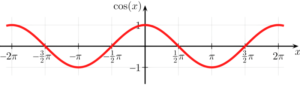
• Su dominio es D(f)= R
• Su recorrido: es el siguiente R(f)= [−1,1]
• También tiene simetría par; esto porque cos (−x) = cos(x)
• Es periódico, su periodo es

Para qué sirve

Al formar parte de las funciones trigonométricas, el coseno nos sirve para poder realizar una serie de mediciones que tengan un mayor grado de precisión. Es aplicado en muchas de las ramas de las matemáticas y en varias disciplinas científicas en las cuales se necesite realizar mediciones exactas. Es muy utilizada en el campo de la astronomía para poder realizar mediciones correctas de las estrellas que se encuentran más cerca de la tierra. También es utilizado en el campo de la geometría del espacio.

Cómo se calcula (formula)

Para calcular el coseno del triángulo existe una fórmula que es muy sencilla. En la fórmula intervienen dos partes fundamentales que forman también parte del triángulo rectángulo, entonces ésta fórmula es la siguiente:

cos x = Adyacente / Hipotenusa

esta fórmula nos indica que la función del coseno es el resultado que se da cuando se divide al lado adyacente del triángulo rectángulo entre la hipotenusa que tenga el mismo triángulo.

Relaciones trigonométricas

El coseno tiene la capacidad de poder ser relacionado con diferentes funciones trigonométricas por medio de las identidades trigonométricas las cuales son un tipo de igualdad que logra unir dos funciones trigonométricas. Es posible encontrar las siguientes relaciones trigonométricas en el coseno:

Relación entre seno y coseno

Implica la curva que tiene el coseno y la curva que posee el seno cuando se desplaza π/2 hacia la izquierda y esto produce la siguiente expresión:

Cos α= sen (α π/2)

Coseno de la suma de los ángulos

En este caso se producen dos expresiones diferentes:

Cos (α + β) = cos α cos β – sen α sen β

Cos (α – β) = cos α cos β – sen α sen β

Suma de funciones como un producto

cos α + cos b = 2 cos ((a+b)/2) cos 2 ((a-b)/2)

cos α – cos b = 2 sen ((a+b)/2) sen 2 ((a-b)/2)

Derivada

La derivada del coseno es un tipo de función que es igual a menos el seno que tiene la función multiplicado por la derivada de la función. Se representa de la siguiente manera:

F (x) = cos u

Integral

La fórmula que se utiliza para poder encontrar la integral del coseno es la siguiente:

∫ cos u du = sin u

Dominio y rango

Para poder conocer el dominio y el rango de una determinada función trigonométrica, en este caso el coseno, primeramente se debe de conocer la forma en la que la gráfica de la función se comporta. También es importante recordar que el dominio de la función coseno implica el uso de números reales. Su fórmula es la siguiente:

f(x) = -3 cos(x) + 1

Función inversa del coseno

Las funciones inversas están relacionadas con las operaciones inversas en donde, por ejemplo, la suma y la resta resultan ser funciones inversas. En el campo de la trigonometría, se sigue la misma idea de manera que, las funciones trigonométricas inversas hacen lo contrario a lo que hacen las funciones trigonométricas normales. En el caso del coseno, su función inversa es la siguiente:

Coseno inverso (cos ⁻¹) hace lo opuesto del coseno

Ejemplos

Algunos ejemplos de coseno se mencionan a continuación:

• Coseno de 270°= -0
• Coseno de 90°= 0°
• De 70° = 0.34202
• De 30°= 0.866025
• De 60° = 0.5
• Coseno de pi°= -1