Cuadriláteros

Es importante mencionar que los cuadriláteros son un tipo muy especial entre los tantos polígonos que existen en el mundo de la geometría.  Tienen una gran cantidad de propiedades diferentes y especiales que los hacen únicos, y que pueden clasificarlos dependiendo de las características que tengan sus lados y sus ángulos.   Cuando tomamos el tiempo para poder analizar su nombre “cuadrilátero” podemos llegar a entender a qué se refiere el término.  El prefijo “cuad-” significa “cuatro,” y “latero” se deriva de la palabra Latina “lado”.  Entonces, podemos decir en otras palabras que un cuadrilátero es un polígono que posee cuatro lados.  Al ser un polígono, sabemos que es una figura que tiene dos dimensiones hechas de lados rectos. Un cuadrilátero tiene cuatro ángulos que están formados por sus cuatro lados.

Temas relacionados

Triángulo rectángulo

¿Qué son los cuadriláteros?

Los cuadriláteros son un tipo de figura geométrica que poseen un total de cuatro lados, éstos lados deben de ser rectos y la figura del cuadrilátero, además, debe de ser de forma bidimensional.

Características de los cuadriláteros

Las principales características que podemos observar en un cuadrilátero son las siguientes:

• Un cuadrilátero tiene 4 lados, 4 y 4 vértices.
• Es un tipo de polígono dentro de la geometría euclidiana.
• Un cuadrilátero puede ser regular o irregular.
• La suma de todos los ángulos interiores de un cuadrilátero es de 360 grados.
• Los cuadriláteros que poseen dos pares de lados paralelos se conocen con el nombre de paralelogramos.
• Los cuadriláteros poseen dos diagonales que se cortan en un punto interior únicamente cuando éste es convexo.
• Poseen también cuatro ángulos.
• Cuando se unen con cuatro segmentos en los puntos medios de los lados que tiene el cuadrilátero, los segmentos forman un paralelogramo.
• Posee los siguientes elementos: 4 vértices o puntos de intersección, 4 lados o segmentos que unen los vértices continuos, 2 diagonales o segmentos cuyos extremos son dos vértices no continuos, 4 ángulos internos que están determinados por lados contiguos, 4 ángulos externos que se determinan por la prolongación de uno de sus lados sobre un vértice y un Unicentro, que es el centro de la circunferencia inscrita.

Propiedades

Las propiedades que podemos encontrar en un cuadrilátero son las siguientes:

• Un cuadrilátero tiene 4 lados, 4 y 4 vértices.
• La suma de todos los ángulos interiores de un cuadrilátero es de 360 grados.
• Todos los lados opuestos del cuadrilátero son paralelos y congruentes.
• Los ángulos del cuadrilátero que son opuestos son congruentes (D = B).
• Los ángulos consecutivos son suplementarios (A + D = 180 °).
• Si un ángulo es correcto, entonces todos los ángulos son correctos.
• Las diagonales de un paralelogramo se bisecan entre sí.
• Cada diagonal de un paralelogramo lo separa en dos congruentes.

Tipos de cuadriláteros

Hay cinco tipos de cuadriláteros que son los siguientes:

• Paralelogramo: Los lados opuestos son paralelos y congruentes, sus ángulos opuestos son congruentes también y sus ángulos adyacentes son suplementarios.  Las diagonales se bisecan entre sí y cada diagonal divide el paralelogramo en dos triángulos congruentes.  Cuando uno de los ángulos de un paralelogramo es un ángulo recto, todos los demás ángulos son correctos y se convierte en un rectángulo.
• Rectángulo: Los lados opuestos del rectángulo son paralelos y congruentes.  Todos sus ángulos son correctos y las diagonales son congruentes dividiéndose entre sí de la misma manera.  Los ángulos opuestos formados en el punto donde se encuentran las diagonales son congruentes.  Es importante mencionar que el rectángulo es un tipo especial de paralelogramo cuyos ángulos son correctos.
• Cuadrado: Todos sus lados y ángulos son congruentes y los lados opuestos son paralelos entre sí.  Las diagonales son congruentes, perpendiculares y se bisecan entre sí.  Un cuadrado es un tipo especial de paralelogramo cuyos ángulos y lados son iguales.
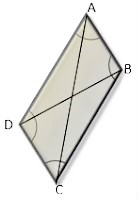
• Rombo:  Todos sus lados son congruentes.  Los ángulos opuestos son congruentes y las diagonales son perpendiculares bisecándose entre sí.  Los ángulos adyacentes son suplementarios.
• Trapecio: Las bases del trapecio son paralelas entre sí  y sus lados, ángulos y diagonales son congruentes.

Historia

Para hablar de la historia de los cuadriláteros se hace necesario referirse a la historia de la geometría.  Los primeros hombres que existieron en la tierra se encargaron de formar figuras geométricas observando la naturaleza.  Los egipcios, fueron los primeros hombres que las utilizaron principalmente para medir sus tierras.  Tiempo después, la geometría se convirtió en el punto fuerte de culturas como la china y la india para la resolución de problemas de distancias y de semejanzas de cuerpo.

Área

El área del cuadrilátero se puede calcular dependiendo de la figura de la que estemos hablando, en estos casos tenemos las siguientes:

• Cuadrado: su área se obtiene multiplicando lado por lado.
• Rectángulo: se calcula lado menor por lado mayor.
• Romboide: se calcula obteniendo el área del rectángulo.
• Rombo: se calcula multiplicando la diagonal mayor por la diagonal menor y luego se divide entre dos.
• Trapecio: el área se calcula con una semisuma de las bases por la altura divido entre dos.
• Trapezoide: se divide el trapezoide en dos triángulos, se calcula el área de cada uno de ellos y se suma.

Perímetro de los cuadriláteros

El perímetro que tienen un cuadrilátero es la longitud que tiene la línea cerrada que se encuentra bordeándolo, en otras palabras, es la suma de las longitudes de sus cuatro lados.

Altura

La altura es definida como la distancia que hay desde un vértice hasta el lado opuesto.  En los cuadriláteros se llama altura media o semialtura de un cuadrilátero a la recta que es perpendicular a un lado que atraviesa el punto medio del lado opuesto.

Ángulos

En los cuadriláteros, la suma de la medida de sus ángulos siempre será de 360°. 

Ejemplos

Rectángulo

Rombo

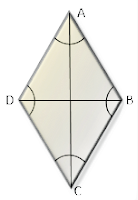
Romboide

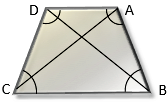
Trapecio isósceles