Centripetal acceleration

Centripetal acceleration is the property of movement that has a body that passes through a circular path. The acceleration is radially directed toward the center of the circle and has a magnitude equal to the square of the velocity of the body along the curve divided by the distance from the center of the circle to the moving body. The force that causes this acceleration is also directed toward the center of the circle and is called the centripetal force.

• Unit: m/s²
• Formula: a_{c = v²/r}

What is centripetal acceleration?

Centripetal acceleration or normal acceleration is the acceleration that determines the change of direction in the velocity in bodies that rotate or move in curves. It is called centripetal because it is always directed toward the center of rotation.

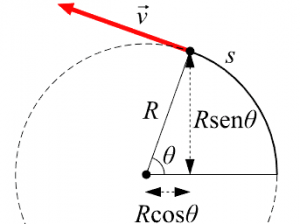
Centripetal acceleration is the idea that any object that moves in a circle, in a circular motion, will have an acceleration vector aiming at the center of that circle. This is true even if the object moves around the circle at a constant speed. It is also important to know that the word centripetal means toward the center.

About centripetal acceleration

It consists of the magnitude linked to the modification that occurs in the direction of a body’s velocity, which moves following a curvilinear trajectory. Before this path, the centripetal acceleration is directed to the center of the curve of the route.

It should be pointed out that when an object moves in a curved form, its speed will always undergo some changes in direction, regardless of whether the speed is constant. This originates because the direction, beyond speed, can never be constant.

A body can make a uniform circular motion and keep the speed constant while at the same time making a circular path. Although speed remains constant, its velocity is not because it is a magnitude that is tangent to the trajectory, and the trajectory repeatedly changes its direction while making the circle.

Centripetal acceleration, therefore, does not change velocity, but it does disturb its direction, making the development of the trajectory possible.

Centripetal acceleration is a type of acceleration that is always present and that is the cause of the tangential velocity, which is located in the part of the contour of the circumference, to suddenly change direction and direction, even if it does not have any influence on its value.

Formula

The formula used to find out the centripetal acceleration of a given object can be calculated as the tangential velocity squared over the radius or as follows:

• a_{c = v²/r}
• a_c = v *ω

Where:

• ac = is the centripetal acceleration [m/s2]
• v = refers to tangential velocity [m/s].
• r = is the turning radius [m].
• ω = is the angular velocity that is equal to 2 π f [rad/s]

How it is measured

Centripetal acceleration can be measured in m/s² or in other words, meters per second every second.

Since the centripetal acceleration force is inversely proportional to the square of the distance, the force will decrease by 2² = four times. Since the force is proportional to the product of the masses, if one of them doubles, the force will double.

The magnitude that represents the intensity of the gravitational field is the acceleration of gravity. For a mass m, with respect to the mass M of the earth is g = F/ m = G – M / R², where G is the constant of universal gravitation.

What is the direction of centripetal acceleration?

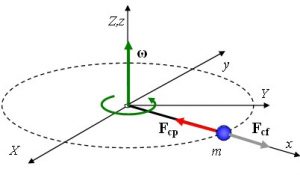
Bodies with a circular motion always have centripetal acceleration, as the direction of velocity changes over time. This acceleration has a type of radial direction and in the direction towards the center of the circumference it describes. This type of acceleration is usually perpendicular to the tangential velocity.

Thus, we can say that the centripetal acceleration will always be pointing to the center of the circle according to Newton’s second Law.

Importance

Centripetal acceleration is an extremely important movement because it is responsible for the fact that the trajectory of a mobile is a circumference.

Examples

Some examples of centripetal acceleration are the following:

• A ball at the end of the string turns evenly in a circle with a radius of 0.60. The ball makes 2.0 revolutions per second. What is its centripetal acceleration?
• When you turn a corner in the car and keep the steering wheel stable during the lap at a constant speed, you move in a uniform circular motion. An acceleration towards the sides is then observed because the person driving and the car change direction. The tighter the curve and the faster it is, the more noticeable the acceleration.