Scalene triangle

Before we refer to the scalene triangle, it is important to know what a triangle itself is. The triangle is a polygon that has three different sides that are responsible for giving rise to three vertices and three internal angles. When we refer to a polygon, we refer to a flat figure that is delimited by different segments. Among the different kinds of polygons, there are triangles: polygons formed by three segments (sides). This is considered one of the simplest figures in the area of geometry and depending on its sides, can be classified into different types.

Related topics

Cathetus, hypotenuse, isosceles triangle, right triangle, Pythagoras

What is the scalene triangle?

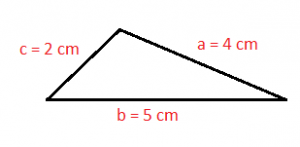
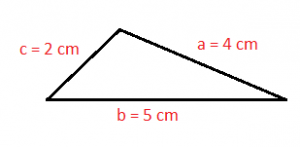
The scalene triangles are those triangles that have three different sides, each one of them with different length. In other words we can say that their three sides are different.

Characteristics of the scalene triangle

The main characteristics of scalene triangles are as follows:

• It is considered as a regular polygon that has three sides and because its sides are all of different size, but it can also be considered as a simple polygon because none of its points come together.
• The three sides of the scalene triangle have different measurements.
• They are triangles that house three interior angles which are also all different.
• It is also considered as a convex polygon.
• They are considered as some of the most resistant geometric figures that exist in the area of geometry.
• This type of geometric figure is considered to be the preferred figure to be used by many builders and architects when standing any building.
• It is important to mention that the term scalene is also used in geometry with reference to scalene trapezoids which, like triangles of this type, have all their sides with different measurements.
• When the scalene triangle is contained in a spherical surface, it is known as a spherical triangle.
• The scalene triangle is also known as the unequal triangle.

Properties

One of its most important properties are its sides because they have lengths of different measures, which is why in this type of triangle you can never show two angles that have the same measure.

When two of the sides of the scalene triangle are summands, the result obtained will always be greater than the length of the third side.

Elements

The scalene triangles have three different elements, and these are known by the name of adjacent cathetus to the angle, opposite cathetus to the angle and hypotenuse. These three elements are always present in a triangle. In addition to these, we can mention the interior of the triangle, which is the inner point of the triangle, the outer boundary which is constituted by the three sides of the triangle, the topological equivalence which says that any triangle will be equivalent to a simple closed curve. The topological equivalence.

The straight line that passes through the vertex of the triangle, the median that is the segment of straight line that goes from the vertex to reach the midpoint of the opposite side and the perpendicular bisector and circumscribed circumference, are three other elements that make up a scalene triangle.

Finally, within the elements of the triangle, the internal and external bisectors, the length of the bisector and the Steiner’s Theorem can also be mentioned.

Height

The height can be calculated when a side (b) is known and the height (h) associated with that side.

Area = (b – h) / 2

Where b is the base and h is the height.

Area

The area of a scalene triangle can be calculated by using Heron’s formula, if the measurements of all its sides (a, b and c) are known.

Area = √ (s (s-a) (s-b) (s-c) )

Where a, b and c are the three sides of the triangle and s the semi perimeter:

s = (a+b+c) / 2

Perimeter

The perimeter of a scalene triangle with three unequal sides is determined by adding the three sides.

Perimeter = a + b + c

Where a, b and c are the three sides of the triangle.

Angles

The angles that the scalene triangles have are completely different and there can never be a triangle within this classification, that has two of its sides of equal measure, they will always be different.

Calculating the sides of a scalene triangle

All sides of the scalene triangle should be measured using different mathematical procedures, as without these measurements it would be impossible to determine the perimeter of the scalene triangle.

How many equal sides does a scalene triangle have?

Remember that scalene triangles do not have any of their sides of equal measure because if so, would be another type of triangle. Related to the sides of the scalene triangle we find the perimeter.

Examples

An example of a scalene triangle is as follows: