Función inyectiva

Cuando hablamos del área de las matemáticas, especialmente en el campo de las funciones, es de suma importancia también saber qué la función es el vínculo que se desenvuelve entre dos conjuntos que son diferentes, vínculo por medio del cual, a cada uno de estos elementos de un conjunto se les asigna un único elemento de otro conjunto o ninguno. La idea de función inyectiva, por otra parte, se refiere a la propiedad que nos indica que a dos elementos diferentes de un primer conjunto le atañen otros dos elementos totalmente diferentes de un segundo conjunto que no es igual al primero.

Temas relacionados

Función biyectiva, función sobreyectiva

¿Qué es la función inyectiva?

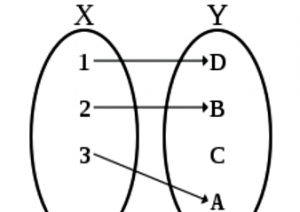
La función inyectiva es el tipo de función de indica que a los elementos diferentes que tiene un conjunto inicial o dominio, le corresponden elementos diferentes del conjunto final o codominio, y cada uno de éstos no tienen una pre-imagen del dominio.

Definición de función inyectiva
Propiedades de la función inyectiva
Aplicaciones
Comprobar si es una función inyectiva
Ejemplos

Definición de función inyectiva

La función inyectiva es también conocida con el nombre de función uno a uno. Una función puede llegar a ser inyectiva si cada uno de los elementos que tiene el conjunto final Y tiene un único elemento del conjunto inicial X al que le corresponde. Esto quiere decir en otras palabras que no pueden haber más de un valor de X que posea la misma imagen Y. No en todas las ocasiones todos los elementos del conjunto final Y deben corresponderse con algún elemento que exista en el conjunto inicial X.

Podemos decir que la función inyectiva se presenta cuando a cada uno de los elementos que tiene el dominio no le corresponde o no pueden tener más de una imagen en el codominio. En el área de las matemáticas, una función f: X ⇒ Y es inyectiva si a elementos que son diferentes del conjunto X o dominio, les corresponden elementos diferentes en el conjunto Y o codominio de f. Esto quiere decir, que cada uno de los elementos del conjunto Y tiene a lo sumo una pre-imagen en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.

Propiedades de la función inyectiva

Entre las propiedades de la función inyectiva mencionamos las siguiente:

La noción de la correspondencia tiene un papel básico en el concepto de relación y de función.
Si n es un número impar, entonces su dominio es todo el conjunto de los números reales.
Si n resulta ser un número par, el dominio estará entonces formado por los valores que hacen que el radicando sea positivo o cero.

Aplicaciones

Las funciones inyectivas nos sirven o se aplican en la graficación correcta de las diferentes funciones; si la función de una sola variable real es inyectiva cualquier línea horizontal cortará sólo en un punto. También se aplican para conocer si la función es invertible. También para poder hacer una clasificación de las transformaciones lineales (monomorfismo inyectiva), epimorfismo (sobreyectiva), isomorfismo (biyectiva).

Comprobar si es una función inyectiva

En matemáticas, una función es inyectiva si dados dos puntos x_a y x_b:

f(x_a) = f(x_b) ⇒ x_a = x_b

Por esta razón podemos decir que la función es inyectiva si logra cumplir con los valores de su dominio x₀ ≠ x₁ ⇒ f(x₀) ≠ f(x₁).

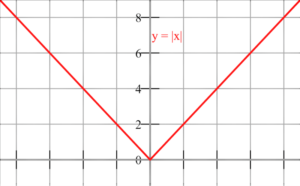
Para comprobar si la función es inyectiva también se puede hacer por medio de la comprobación gráfica de la inyectividad de la función, y esto se hace cuando en cualquier recta que sea paralela al eje X, corta a la misma recta, como máximo, en un punto.

Ejemplos

Algunos ejemplos de la función inyectiva que podemos observar en nuestra vida diaria son los siguientes:

Cuando se conecta en una amplificador los cables, no todos los orificios que existen van a quedar conectados a uno de los cables pero sí lo hacen algunos, y nunca va a haber dos conexiones en un mismo orificio.
Cuando se determinan los identificadores de los usuarios, a cada uno de estos usuarios le va a corresponder un único identificador y no puede haber dos usuarios que posean el mismo id.

También son funciones inyectivas: