Función sobreyectiva
En el área de la matemática, una función es una relación que existe entre un conjunto dado X también conocido con el nombre de dominio y otro conjunto de elementos Y, que se conoce con el nombre de codominio, de manera tal que a cada elemento x del dominio le corresponde un único elemento f (x) del codominio. La función, definida en un lenguaje más simple y sencillo es un proceso lógico común que se expresa como “depende de”. Las funciones pueden ser clasificadas dependiendo de la relación que guardan entre sí los elementos que tenga el dominio, del codominio y de la imagen. Las funciones matemáticas en la vida real pueden referirse a situaciones cotidianas, como por ejemplo el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso. Una función es una relación entre dos conjuntos en la que a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto. Una función sobreyectiva, también conocida con los nombres de función suprayectiva, epiyectiva o suryectiva es una función en la que cada valor resultado tiene al menos un valor de origen.
¿Qué es una función sobreyectiva?
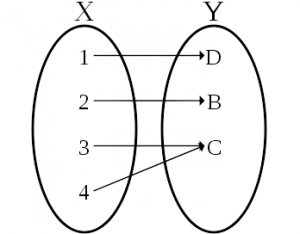
Decimos que una función es sobreyectiva o suprayectiva si todos los elementos que están en la imagen, Y tienen anti-imagen. En otras palabras, si para cualquier y de la imagen Y existe al menos un elemento x de la imagen tal que f(x) = y.
Definición de función sobreyectiva
Una función es sobreyectiva, suprayectiva o exhaustiva, se presenta cuando el codominio y el recorrido coinciden. Formalmente, se puede definir de la siguiente manera:
∀y ∈ Cod f ∃ x ∈ Dom f | f(x) = y
Esto quiere decir, para cualquier elemento y para el codominio existe otro elemento x del dominio tal que y es la imagen de x por f. En matemática, una función es sobreyectiva, si está aplicada sobre todo el codominio, es decir, cuando cada elemento de «Y» es la imagen de como mínimo un elemento de «X». Para que sea un poco más fácil de entender, podemos decir que cada conjunto o elemento de partida tiene que cubrir a los elementos del codominio o conjunto de llegada. Cada valor en una función sobreyectiva tiene que tener su pareja respectiva en el conjunto de llegada para que sea una función sobreyectiva.
Propiedades de la función sobreyectiva
Entre las propiedades de la función sobreyectiva mencionamos las siguientes:
Tiene dominio de la función el cual es el conjunto de los valores que puede tomar la variable independiente, es decir, aquellos valores para los que la función está definida.
Con respecto a la imagen de la función tiene crecimiento, que incluye la creciente que ocurre si al aumentar la x, la y también se ve aumentada; y decreciente, que sucede si al aumentar el valor de x, el valor de y. Además tiene constante, si al variar x, la y se mantiene igual.
Aplicaciones
En nuestra vida cotidiana, la función sobreyectiva puede y es aplicada en diferentes situaciones cotidianas. Por ejemplo es utilizado en problemas de optimización en los planteamientos de problemas de estructura multiplicativa o del agente viajero, donde se tienen que ocupar todos los nodos que van del lado 1 al lado 2. En el área de las finanzas cuando a cada portafolio de inversión le corresponde uno o más inversionistas.
Imaginemos por ejemplo, que nos encontramos en un almacén o un supermercado en donde existen muchos y diferentes productos, cada producto que se encuentra en el supermercado posee un único código de barra y que únicamente le pertenece a ese producto. El punto de partida acá son los productos y los conjuntos de llegada serán los códigos de barra. Esto quiere decir que para producto que está en el supermercado, únicamente existe un código de barra.
Cómo saber si es una función sobreyectiva
Sabemos que una función es sobreyectiva ó suryectiva cuando cada uno de los elementos que existen dentro del rango, es la imagen, de al menos un elemento del dominio de dicha función. Otra forma de determinar cuando una función es sobreyectiva es si todo elemento del conjunto final Y tiene por lo menos un elemento del conjunto inicial X al que le corresponde. Esto quiere decir que, una función es sobreyectiva si el recorrido de la función es el conjunto final Y.
Ejemplos
Algunos ejemplos de la función sobreyectiva son los siguientes:
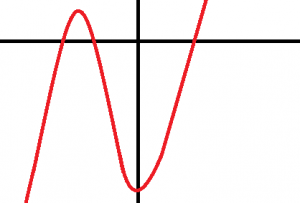
- Las siguiente función es sobreyectiva porque todos los números que se encuentran en el recorrido de la función son números reales:
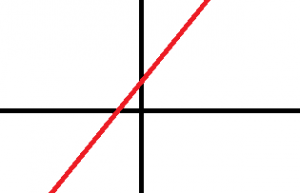
- Por el mismo motivo, la siguiente también es sobreyectiva:
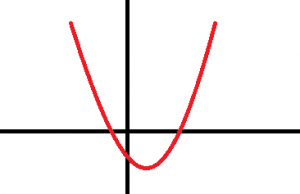
- Ejemplo de función que no es sobreyectiva:
¿Cómo citar este artículo?
Briceño V., Gabriela. (2018). Función sobreyectiva. Recuperado el 4 mayo, 2025, de Euston96: https://www.euston96.com/funcion-sobreyectiva/