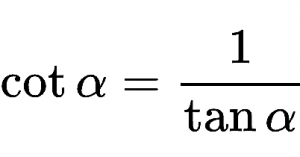Mediatriz

En el área de la geometría existen diferentes e importantes aplicaciones y una de ellas es la mediatriz, la cual es utilizada para poder hacer una determinación del circuncentro de los polígonos cíclicos, esto porque por definición, la recta que pasa por el punto medio de un segmento que está ubicado dentro de la circunferencia inscrita en el polígono necesariamente pasará por su centro. Cuando nos referimos a una circunferencia, cualquier mediatriz de una cuerda que pertenezca a esta pasará por su centro. La mediatriz es uno de los objetos geométricos más importantes en otras construcciones más complejas.

Temas relacionados

Bisectriz

¿Qué es la mediatriz?

En geometría, conocemos con el nombre de mediatriz de un segmento a la recta que tiene como función la de cortar a un segmento de forma perpendicular por su punto medio.

Definición

La mediatriz de un segmento es la recta perpendicular a ese segmento que pasa por su punto medio. Cuando tenemos un segmento AB, la mediatriz de ese segmento es una recta de forma perpendicular que pasa por el medio.

Conocemos con el nombre de mediatriz, en el área de la geometría, a la recta que es dibujada desde un punto medio de un segmento y que además cumple con la condición de perpendicularidad con respecto a ella. Su efecto principal incurre en que los dos lados que genera el segmento son completamente proporcionados con respecto al punto medio donde se traza la mediatriz.

Si lo vemos desde el punto de vista analítico, la mediatriz se puede describir como una recta en la cual sus puntos que la conforman se encuentran equidistantes a los extremos del segmento, es importante señalar que la mediatriz la poseen solo segmentos por lo que no puede ser aplicada a conceptos infinitos no definidos.

Características

Las características más sobresalientes que tiene una mediatriz son las siguientes:

• Las rectas mediatrices son también conocidas con el nombre de simetral.
• Cuando se construyen ángulos, se genera la bisectriz del que está formado entre dos puntos equidistantes con respecto al punto medio y por donde pasa la mediatriz.
• Es una recta perpendicular.
• Divide el ángulo por la mitad.
• Pasa siempre por el punto medio del segmento.
• Las dos partes que resultan de la división del segmento miden lo mismo.
• La mediatriz de un segmento puede ser construida con una regla y un compás.
• Puede ser llamada también como lugar geométrico.
• Existen tres mediatrices en un triángulo (Ma, Mb y Mc), según el lado del triángulo al que se refieren (a, b o c).

Propiedades

Al igual que muchos temas dentro del área de la geometría, la mediatriz tiene propiedades que mencionamos a continuación:

• Un punto cualquiera de la mediatriz se encuentra a la misma distancia en la que se encuentran los dos extremos del segmento.
• Si dos circunferencias son tangentes, el punto de tangencia está en la recta.
• Si una recta es tangente a una circunferencia, el punto de tangencia se encuentra ubicado en la perpendicular a r trazada por O.
• Si una circunferencia pasa por dos puntos, su centro se localiza en la mediatriz del segmento que une estos puntos.
• Si una circunferencia es tangente a dos rectas su centro está en la bisectriz del ángulo que forman dichas rectas.

Cómo se traza la mediatriz

Para lograr trazar la mediatriz, debemos de seguir una serie de pasos importantes que son los siguientes:

• Es importante saber que para poder trazar la mediatriz vamos a necesitar el uso de un compás.
• El compás debe de abrirse algo más de la mitad del segmento dado AB y, debe tener su centro en el extremo A donde se traza una arco.
• Manteniendo la abertura del compás y sin producir ningún tipo de modificación y con el centro en B, se debe de trazar otro arco que cortará al anterior en los puntos C y D.
• Para finalizar, se deben unir los puntos C y D para obtener la recta mediatriz.

Mediatriz de un ángulo

La mediatriz únicamente se puede aplicar los extremos de los segmentos y no a los ángulos.

Mediatriz de un triángulo

Conocemos como la mediatriz de un triángulo a la mediatriz que se encuentra asociada a uno de sus lados, esto quiere decir, la recta perpendicular a dicho lado que pasa por el punto medio o por el centro de éste. En el triángulo podemos encontrar tres mediatrices en un triángulo, que son Ma, Mb y Mc, dependiendo del lado del triángulo al que se refieren (a, b o c).

Las tres mediatrices que podemos encontrar en un triángulo coinciden en un punto que es conocido con el nombre de circuncentro. Este circuncentro es entonces el centro de la circunferencia circunscrita en el triángulo, ya que equidista de sus tres vértices.

Mediatriz de un segmento

La mediatriz de un segmento es la línea recta perpendicular a dicho segmento que ha sido trazada por su punto medio y que lo divide en dos partes completamente iguales. Podríamos decir también que es el lugar geométrico o la recta, cuyos puntos son equidistantes a los extremos del segmento.

Ejemplos

Algunos ejemplos de la mediatriz son los siguientes:

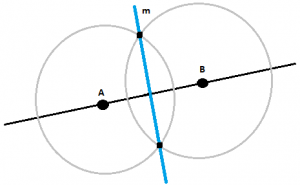
• La recta m es la mediatriz del segmento AB ya que pasa por el punto medio perpendicularmente formando cuatro ángulos rectos (90º).

• Sea el segmento AB de la recta r. Para obtener la mediatriz del segmento AB dibujamos dos circunferencias, una con centro en el punto A y otra con centro en el punto B. Las dos deben tener el mismo radio. Marcamos los dos puntos de corte de las dos circunferencias. Unimos los dos puntos de corte de las circunferencia y obtenemos la recta m que es la mediatriz del segmento AB, perpendicular al m.