Momento angular

El momento angular es una propiedad que posee la masa que se encuentra en movimiento alrededor de un eje determinado, que en un dominio cerrado se conserva. Cuando hablamos de la atmósfera, el momento angular es un parámetro bastante útil para lograr hacer estudios de la dinámica en diferentes escalas, ya sean temporales o espaciales. Cuando el eje de referencia se identifica con el de la figura de la Tierra, que podemos llamar el eje principal, el valor del momento angular axial globalmente integrado resultante, además, puede tratarse como un índice fundamental de la circulación atmosférica. Como tal, este parámetro refleja muchos aspectos de la firma del clima y el clima.

• Unidad: Kg m²/s
• Fórmula: P = mv

¿Qué es el momento angular?

El momento angular es una magnitud vectorial que se encarga de señalar el estado de rotación que tienen los cuerpos alrededor de un punto determinado y es parte de la mecánica clásica, cuántica y relativista.

Definición

Es una de las magnitudes del área de la física más importantes. Se define como la cantidad de movimiento que está asociado a un objeto que realiza una rotación alrededor de un punto determinado o un punto fijo. El movimiento angular puede darse en torno al centro de masas propios del objeto y por esta razón, cuando se busca el momento angular, es también importante conocer el momento de inercia que posee un cuerpo.

Cuando nos referimos al momento angular de la tierra, decimos que es la suma de su momento angular sobre su eje propio alrededor de un eje imaginario que se ubica en el centro de masas del sistema Tierra-Sol. El momento angular es una magnitud que siempre se conserva, es la suma del momento angular que es transferido de un cuerpo hacia otro dentro de un sistema cerrado que siempre será cero, por esta razón, la cantidad de energía que se transfiere a otro cuerpo siempre será igual a la cantidad que es recibida por otros cuerpos.

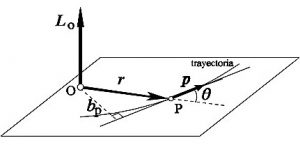
Momento angular de una partícula

El momento angular de una partícula puede ser definido como el producto vectorial del vector posición r por el vector momento lineal mv. Se debe de medir en SI en Kg m²/s. Esto se puede representar por medio de la fórmula:

P = mv

En donde m es la masa y v es la velocidad que tiene la partícula. Esta ecuación puede también ser reescrita como L = mrxv. La letra L se refiere a la magnitud vectorial perpendicular a r y a v. X se refiere al ángulo que forman r y v. Cada vez que r y v sean paralelas entre sí, nos indica que el momento angular de la partícula es cero.

Momento angular de un cuerpo rígido

Las partículas que encontramos en un sólido rígido que se encuentra en rotación alrededor de un eje fijo describen circunferencias que están centradas en el eje de rotación y que poseen una velocidad que es proporcional al radio de la circunferencia que describen:

V_i = wr_i

El momento angular que poseen los cuerpos rígidos vale:

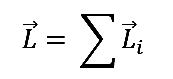
La proyección L_z del vector momento angular a lo largo del eje de rotación es:

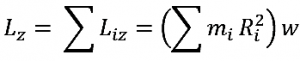
Momento angular orbital

Cuando hablamos del momento angular orbital nos referimos al momento angular de los electrones que encontramos en los átomos, los cuales se encuentran asociados a un determinado estado cuántico, y están cuantizados de la siguiente manera:

En donde l es el momento angular cuántico del número y es también 0, 1, 2… n-1.

Podemos decir que este es el resultado de aplicar la teoría cuántica a la órbita que posee el electrón. La solución de la ecuación de Schrödinger nos brinda el número cuántico del momento angular.

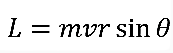
Conservación

En el área de la física llamamos con el nombre de momento de una fuerza respecto de un punto, al producto vectorial del vector posición de la fuerza por el vector fuerza. En cuanto a la conservación del momento angular existe un principio importante de conservación del momento angular, el cual afirma que si el momento de las fuerzas exteriores es igual a cero (situación que no implica que las fuerzas exteriores sean cero, que sea un sistema aislado), el momento angular en su totalidad se conserva, en otras palabras, permanece constante. Su fórmula es la siguiente:

dL / dt = M_ext

M_{ext = 0}

L = cte

Relación con el torque

Es importante saber que una torca es una medida de fuerza que logra hacer que un determinado objeto gire alrededor de un eje. La torca entonces es la responsable que hacer que un objeto logre adquirir una aceleración angular. Es una cantidad vectorial y la dirección que tiene el vector de la torca depende de la dirección de la fuerza del eje. El torque produce una variación o un cambio en el momento angular de un grupo de partículas o también puede darse en un objeto rígido.

Ejemplos

Un ejemplo sería una lata de refresco que va rodando por una calle que tiene una pendiente o también la rueda de una bicicleta que sigue girando hasta ser detenida por alguna cosa. En estos dos ejemplos podemos decir que tienen momento angular.