Número e

El número e, número de Euler o como también es conocido, constante de Napier es uno de los número irracionales que tiene mayor relevancia e importancia en el área de las matemáticas y álgebra. Un número básico en las funciones exponenciales que no puede ser expresado en números naturales.

Temas relacionados

Número áureo, número pi

¿Qué es el número e?

El número e, es un número irracional del cual no podemos averiguar el valor exacto que posee ya que tienen una cantidad infinita de cifras decimales y por esto es considerado como irracional.

Definición

En el área de las matemáticas, podemos definir el número e como la base de la función exponencial natural, que en algunas ocasiones es también conocida como la base neperiana, esto porque fue el matemático neper el primero en utilizarla. El número es conocido como un número irracional debido a que no puede ser expresado por la razón de dos números enteros, sus números decimales son y infinitos además, es un número trascendente ya que no puede ser expresado como la raíz de ecuaciones algebraicas con coeficientes racionales.

Características el número e

Entre las principales características del número e, podemos mencionar las siguientes:

• Es un número poco llamativo y sus cifras no se pueden repetir de forma periódica.
• Las cifras del número e no siguen ningún tipo de pauta.
• Es por lo general conocido con el nombre de constante de Napier o el número de Euler.
• Puede ser utilizado en diferentes ramas del área de la matemática.
• No puede ser expresado utilizando dos números enteros.
• Tampoco puede expresarse como un número decimal exacto o un decimal periódico. 

Origen

El conocido e importante matemático llamado Leonhard Euler , uno de los matemáticos más prolífico de todos los tiempos, utilizó en el año 1727 la notación e en relación con la teoría de los logaritmos. La coincidencia entre la primera letra de su apellido y el nombre de nuestro número es mera casualidad. 

Historia

La primera vez que se encuentra un registro o una aproximación del número e en un tratado matemático data del año 1614, en el que se publica el Mirifici Logarithmorun Canonis de John Napier. A pesar de esto, la primera aproximación que se realizó con respecto al número fue obtenida por medio e Jacob Bernoulli en la solución del problema del interés a largo plazo de una cantidad fija inicial que lo llevó a conocer e investigar sobre el Limite fundamental algebraico, y cuyo valor fijó en 2.7182818. Leonard Euler fue quien comenzó a identificar el número con su símbolo actual, el cual corresponde a la letra e, pero lo logró presentar a la comunidad matemática en su libro Mechanica, aproximadamente 10 años después.

Quién descubrió el número e

En realidad el número fue descubierto primeramente por Leonhard Euler pero fue el escocés llamado John Napier quien descubrió este número que en realidad es una herramienta matemática en el año 1614. En un apéndice de su trabajo, aparece su constante base, el número e, que hoy podemos ver en todas las calculadoras. Fue gracias a su descubrimiento que las multiplicaciones pueden ser sustituidas por sumas, las divisiones por restas y las potencias por productos, simplificando la realización manual de los cálculos matemáticos.

Propiedades

Las propiedades siguientes también pueden ser tomadas como definición de e.

• e es la suma de los inversos de los factoriales.
• e es el límite de la sucesión de término general.
• el desarrollo decimal de e no tiene ninguna regularidad alguna pero con las fracciones continuas, que pueden ser normalizadas o no, obtenemos, en fracción continua normalizada.
• e es irracional y trascendental.

Aplicaciones

Algunas de las aplicaciones en las que puede llegar a ser utilizado el número e son las siguientes:

• En economía, que de hecho fue la primer área en donde fue para calcular intereses compuestos.
• En biología donde resulta muy importante para poder describir el crecimiento celular.
• En electrónica para realizar descripciones sobre la descarga de un condensador.
• En el área de la química para describir concentraciones de iones o el desarrollo de una reacción.
• Para trabajar con los números complejos, principalmente en las fórmulas de Euler.
• En paleontología para realizar la datación de fósiles por medio del Carbono 14.
• En medicina forense para medir la pérdida de calor de un cuerpo inerte y así conocer el momento de su muerte.
• En estadística, en la teoría de probabilidad y en la función exponencial
• En la razón áurea y la espiral logarítmica.
• Por aparecer en la función exponencial, que modela el crecimiento, su presencia es importante cuando estudiamos el crecimiento o decrecimiento acelerados, como pueden ser las poblaciones de bacterias, la propagación de enfermedades o la desintegración radioactiva, lo que es también de utilidad en la datación de fósiles.

Cuánto vale

El número e equivale a 2.71828 aproximadamente lo que generalmente se escribe como ≈ 2,718.

Cómo se representa el número e

El número e se puede representar de la siguiente manera:

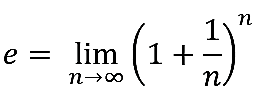
Importancia

El número e es muy importante dentro del área de las matemáticas y en muchos otros sectores que se encuentran relacionados con la producción, ciencia y la vida cotidiana. El número e juega un papel de suma importancia en el área del cálculo, y forma parte de muchos de los resultados fundamentales de límites, derivadas, integrales, series, etc. Además, posee una serie de propiedades que hacen que se pueda utilizar en la definición de expresiones de gran aplicación en muchas áreas del conocimiento humano.

Curiosidades

Algunas curiosidades relacionadas con el número e son las siguientes:

• El número e funciona como base del sistema de logaritmos neperianos o naturales.
• El número se denota por lnx = t, donde x es un número real positivo y t es positivo para x>1 y negativo para x <1.
• Se hace presente en la definición de la función y(x) = ex, o bien y(x) = exp(x), siendo su conjunto de valores admisibles CVA el conjunto R de todos los números reales.