Propiedad conmutativa

Si analizamos los operadores matemáticos podemos comprobar que los mismos cuentan con distintas propiedades. Estas nos hablan del modo en que se pueden distribuir, asociar o conmutar los números a la hora de realizar una operación. En esta ocasión vamos a centrarnos en la propiedad conmutativa la cual nos permite, si lo deseamos, alterar el orden de los sumandos en la suma y de los factores en la multiplicación sin que el resultado se vea alterado. Algo que debemos destacar es la importancia que tiene esta propiedad, pues gracias a la misma podremos evitar errores a la hora de resolver ecuaciones y operaciones matemáticas.

Ejemplo rápido

• Suma
  • 2 + 6 + 1 = 9
  • 6 + 1 + 2 = 9
• Multiplicación
  • 3 x 2 x 4 = 24
  • 4 x 3 x 2 = 24

¿Qué es la propiedad conmutativa?

La propiedad conmutativa es una propiedad matemática que tienen tanto la suma como la multiplicación. Esta nos indica que no importa cual sea el orden en el que se suman los sumandos o se multiplican los factores pues el resultado obtenido no se verá alterado.

Propiedad conmutativa de la suma

Definición: «El orden de los sumandos no altera la suma»

La propiedad conmutativa de la suma, también denominada propiedad del orden de la suma, es aquella que nos permite que los sumandos o cifras de una suma o adición puedan ser intercambiados sin que el resultado se vea afectado. Es decir, podemos realizar la suma en el orden que queramos pues el resultado que obtendremos siempre será idéntico.

Ejemplos

Vamos a sumar 2, 3 y 5 en distinto orden para ver que el resultado es el mismo:

• 2 + 5 + 3 = 10
• 3 + 5 + 2 = 10
• 5 + 3 + 2 = 10

Por tanto tenemos que:

2 + 5 + 3 = 3 + 5 + 2 = 5 + 3 + 2 = 10

Como vemos, se cumple la propiedad conmutativa pues por mucho que alteremos el orden el resultado siempre es 8. Y es que no importa el orden en el sumamos los distintos números pues en ningún caso afecta al resultado.

Veamos otro ejemplo.

Ahora sumaremos los números 2, 4 y 6 alterando el orden para comprobar si da el mismo resultado:

• 2 + 4 + 6 = 12
• 4 + 6 + 2 = 12
• 6 + 2 + 4 = 12

Es decir:

2 + 4 + 6 = 4 + 6 + 2 = 6 + 2 + 4 = 12

Al igual que en el ejemplo anterior, vemos que sea cual sea el orden en el que decidimos realizar la operación el resultado es exactamente el mismo.

Ejercicios

[HDquiz quiz = «870»]

Propiedad conmutativa de la multiplicación

Definición: «El orden de los factores no altera el producto»

La propiedad conmutativa de la multiplicación o propiedad del orden de la multiplicación, es la propiedad matemática que nos indica que los distintos factores de una multiplicación pueden ser acomodados en el orden que deseemos, pues sea cual sea este, el resultado que obtendremos será el mismo.

Ejemplos

En este ejemplo multiplicaremos los números 2, 3 y 5 en distinto orden.

• 2 x 3 x 5 = 30
• 3 x 5 x 2 = 30
• 5 x 2 x 3 = 30

Por tanto:

2 x 3 x 5 = 3 x 5 x 2 = 5 x 2 x 3 = 30

Multiplicamos 3, 4 y 6 modificando su orden ¿El resultado es el mismo?

• 3 x 4 x 6 = 72
• 6 x 3 x 4 = 72
• 4 x 6 x 3 = 72

Obtenemos que:

3 x 4 x 6 = 6 x 3 x 4 = 4 x 6 x 3 = 72

Ejercicios

[HDquiz quiz = «871»]

Propiedad conmutativa de la resta

La resta se compone de dos partes, el minuendo y el sustraendo, y si tratamos de alterar su orden veremos como el resultado que obtenemos no es el mismo y es que la propiedad conmutativa no aplica en el caso de la resta. Visto esto, podemos concluir que cualquier cambio que realicemos en el orden de los elementos de una resta ocasionarán que también cambie el resultado de la misma.

Ejemplo

Vamos a restar 8 y 2 en distinto orden para ver si el resultado que obtenemos es el mismo o no:

• 8 – 2 = 6
• 2 – 8 = -6

Por lo que tenemos que:

8 – 2 ≠ 2 – 8

Como vemos el resultado de restar 2 a 8 no es igual que el de restar 8 a 2, por lo que se cumple el hecho de que la propiedad conmutativa no aplica a la resta.

Propiedad conmutativa de la división

Con la división pasa lo mismo que con la resta pues no se puede aplicar la propiedad conmutativa ya que si cambiamos el dividendo por el divisor veremos como el resultado no será el mismo. Vamos a ilustrar esto con un ejemplo.

Ejemplo

En este ejemplo vamos a dividir 8 y 4 alternando el orden y comprobaremos si el resultado obtenido es el mismo o no.

• 8 : 4 = 2
• 4 : 8 = 0,5

Tal y como se puede comprobar el resultado es diferente en cada caso por lo que no podemos aplicar la propiedad conmutativa a la división.

Propiedad conmutativa de las matrices

En el caso de las matrices esta propiedad se cumplirá únicamente en el caso de que lo que realicemos sea una suma. Si vamos a realizar una multiplicación de matrices, debemos saber que la propiedad conmutativa no se podrá aplicar salvo en situaciones muy concretas. Veamos esto con un ejemplo.

Ejemplo

Vamos a multiplicar la matriz A  y la matriz B modificando su orden y analizaremos el resultado obtenido.

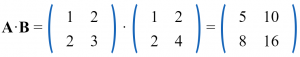
Si nos fijamos en el resultado de ambas multiplicaciones nos daremos cuenta que los resultados son diferentes por lo que A · B ≠ B · A así que la propiedad conmutativa no se cumple.

Para qué sirve

Esta propiedad matemática nos facilita la vida a la hora realizar operaciones ya que nos permite ordenar los números de la manera que mejor nos convenga a la hora de realizar sumas o multiplicaciones y todo ello sin modificar el resultado final. Uno de los principales usos que recibe es el de ayudarnos a resolver ecuaciones con incógnitas, pues esta propiedad nos facilita la resolución de las partes más complicadas. También resulta especialmente útil cuando tratamos de sumar matrices, polinomios o vectores, e incluso puede ser utilizada en campos distintos al de las matemáticas como es de la lógica proposicional en operaciones relacionadas con la teoría de conjuntos, o el de la física donde puede aplicarse al principio de incertidumbre.

Historia

La historia de la propiedad conmutativa se fundamenta en el álgebra, la cual es la rama de las matemáticas que estudia la forma de combinar los elementos de las estructuras de acuerdo con ciertas reglas, ya sean números o cantidades. Las raíces de la palabra álgebra se pueden rastrear a la antigua matemática babilónica en donde se logó desarrollar un sistema aritmético con el cual fueron capaces de realizar cálculos en forma algorítmica. La conmutatividad ya era conocida en la antigüedad en las operaciones elementales, sumar y restar. Por medio de las consecuentes ampliaciones que sufrió el concepto de número, se amplió el alcance de las operaciones de sumar y de multiplicar.

¿A qué sistemas numéricos se aplica la propiedad conmutativa?

La propiedad conmutativa de la suma y la multiplicación se cumple en los distintos sistemas numéricos por lo que se puede aplicar a los números naturales, enteros, reales, racionales, algebraicos y complejos.

Propiedades relacionadas

La simetría y la asociatividad son dos propiedades que están estrechamente relacionadas con la propiedad conmutativa.

La primera de ellas, la simetria, nos dice que una operación matemática es simétrica cuando tras realizar una alteración en la misma el resultado obtenido es el mismo. Esto es precisamente lo que ocurre con los operadores suma y multiplicación en los cuales se aplica la propiedad conmutativa. En estos casos alternamos el orden de los factores o de los sumandos y pese a ello el resultado que logramos es el mismo.

En cuanto a la propiedad asociativa, esta nos indica que a la hora de realizar una suma o una multiplicación de tres números o más no importa el orden en que realicemos las operaciones pues llegaremos siempre al mismo resultado. Es decir, si sumamos 2 + 1 + 3, podemos hacer primero 2 + 1 y luego sumar 3, o sumar primero 1 + 3 y luego sumar el 2 y el resultado será el mismo.

(2 + 1) + 3 = 2 + (1 + 3)

Como hemos visto la propiedad conmutativa es similar a la asocitariva, pero en este caso hace referencia al orden de los términos y no al orden en el que se realiza la operación. Debemos destacar que, por lo general, en las operaciones en las que se cumple la conmutatividad también se cumple la asociatividad, aunque en realidad que se de una no implica que la otra también se de.

Temas relacionados

• Propiedad asociativa
• Propiedad distributiva