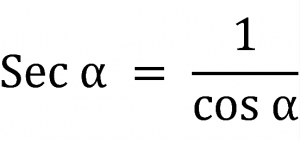Secante

La trigonometría es una de las subdivisiones de las matemáticas que se encarga de calcular los elementos que tienen los triángulos. Y es por esta razón que se dedica a estudiar las relaciones que pueden haber entre los ángulos y los lados de los triángulos. Hay seis funciones importantes que son consideradas como el núcleo de la trigonometría. Tres de ellas son catalogadas como las principales y son el seno, coseno y tangente. Las otras tres funciones trigonométricas son menos frecuentes pero igual de importantes y su cálculo no se encuentra tan fácilmente como en el caso de las tres primeras que pueden ser encontradas por medio de una calculadora, y éstas son la secante, la cosecante y la cotangente.

Temas relacionados

Cosecante, cotangente, teorema del coseno

¿Qué es la secante?

En un triángulo rectángulo podemos decir que la secante es una función de trigonometría que se refiere a la longitud que existen en la hipotenusa y que es dividida por la longitud del lado adyacente.

Definición

La definición de razones trigonométricas, como es el caso de la secante, se refiere a los vínculos que se pueden llegar a establecer entre los diferentes lados que tiene un triángulo que dispone de un ángulo de 90º. Entre estas razones podemos encontrar, aparte de las tres principales, tres diferentes que se conocen con el nombre de razones trigonométricas recíprocas, entre ellas tenemos el caso de la secante.

La secante de un ángulo se define como la relación que existe entre la longitud de la hipotenusa y la longitud del cateto adyacente, en otras palabras:

sec α = hipotenusa/adyacente

Características de la secante

Sus principales características son las siguientes

• El dominio de la función secante es el de conjunto: {x Є R / x ≠ pi / 2 + n π, n Є Z }
• Como sec x ≤ -1 y seg x ≥ 1, decimos entonces que el Rango de la Función es el Conjunto R – (-1,1)
• La función secante es par, pues sec (-x) = sec x, entonces, la gráfica es simétrica con respecto al eje y.
• y = sec x es una función periódica y su Periodo es 2π .
• La función y = sec x es creciente en los Intervalos en el los cuales y = cos x es decreciente. y es decreciente cuando cos x es creciente, es decir, en el los Intervalos [ π , 3π/ 2 ) y ( 3π/ 2 , 2 π ].
• La función y = sec x no tiene valor máximo ni un valor mínimo y nuca se anula, es decir, no tiene ceros.
• y=sec x es una función continua en todo su dominio, es decir en el conjunto .
• {x Є R / x ≠ pi / 2 + n π, n Є Z }.

Para qué sirve

Las funciones trigonométricas como en el caso de la secante nos sirven para poder calcular grados, ángulos y otros datos geométricos con respecto a una determinada figura geométrica. La secante también es usada para poder encontrar la medida de los lados que tiene triángulo un o la medida de sus ángulos como medida inversa que es.

Todas estas funciones tienen su importancia en el estudio de la geometría de los triángulos y en la búsqueda de formas para representar los fenómenos periódicos. Son por lo general utilizadas para realizar cálculos técnicos, para topografías en la tierra y para marcar cada ángulo utilizando un determinado punto de referencia.

Cómo se calcula la secante

La secante que en su forma abreviada se escribe como sec, es la razón trigonométrica recíproca del coseno, o también su inverso multiplicativo y su fórmula es la siguiente:

Sec α = 1 / cos α = c / b

Derivada

Se conoce como la derivada de la secante a la misma función que es igual a la secante de la función por la tangente de la función, y por la derivada de la función.

f (x) = sec w

f ‘(x) = ( w’ · sen w ) / cos² w

Integral

La integral de secante de una función se deriva de dicha función. Podemos decir que es el resultado de dicha integral es logaritmo natural de la suma que se da entre la secante y tangente de la función. Este resultado no puede ser obtenido por medio de la derivación inmediata de una función conocida.

Dominio y rango de la secante

Los dominios tanto de la cosecante y como de la secante se encuentran restringidos y únicamente pueden ser utilizadas las funciones para medidas de los ángulos con los números de salida que existen. Cada vez que el lado del terminal de un ángulo se encuentra a lo largo del X-eje en el cual y = 0, no se puede llegar a realizar la función cosecante en ese ángulo.

Función inversa

En el área de la trigonometría, conocemos con el nombre de arcosecante a la función inversa que tiene la secante de un ángulo. Se simboliza como “arsec α” y su significado geométrico es el ángulo cuya secante es alfa.