Triángulo rectángulo

Los triángulos son polígonos que están formados por tres lados por lo que podemos decir que el triángulo es una figura plana que está formada por tres segmentos diferentes.

Temas relacionados

Cateto, hipotenusa, teorema de Pitágoras, Pitágoras, triángulo escaleno, triángulo isósceles, cuadriláteros

¿Qué es el triángulo rectángulo?

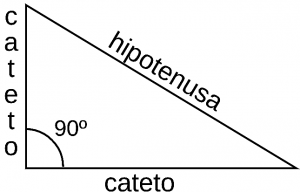
El triángulo rectángulo es el triángulo que tiene un ángulo recto el cual tiene una medida de 90 grados y dos ángulos que son agudos, lo que quiere decir que miden menos de noventa grados.

Características del triángulo rectángulo

Las características más importantes de los triángulos rectángulos son:

• Son polígonos que tienen tres lados.
• Están formados por tres segmentos.
• Todos tienen un ángulo recto de noventa grados.
• Los dos ángulos que no son rectos siempre serán ángulos agudos.
• El ángulo recto está conformado por los dos lados de menor longitud.
• Pueden ser triángulos isósceles o escalenos.

Propiedades

Los triángulos rectángulos tienen varias propiedades que a continuación se mencionan:

• Todos tienen dos ángulos agudos y su hipotenusa es más grande que los catetos.
• El cuadrado de la hipotenusa es igual a la suma del cuadrado de los catetos.
• La suma de la hipotenusa y el diámetro de un círculo inscrito en el triángulo es igual a la suma de los catetos.
• Cuando calculamos el área, un cateto puede ser considerado como base y el otro cateto como altura.
• La mediana de la hipotenusa descompone un triángulo rectángulo escaleno en dos triángulos.
• La mediana de la hipotenusa de un triángulo rectángulo isósceles lo descompone en dos triángulos rectángulos isósceles congruentes y equivalentes.
• Dos triángulos rectángulos que tengan una hipotenusa común, y los ángulos rectos en semiplanos opuestos determinados por la recta que contiene a la hipotenusa, forman un cuadrilátero birrectángulo.
• La mediana que parte del ángulo recto es igual a la mitad de la hipotenusa.

Tipos de triángulo rectángulo

Existen dos diferentes tipos de triángulos rectángulos, éstos son:

• Triángulo rectángulo isósceles: es el triángulo que tiene un ángulo recto de 90º y dos ángulos de 45º. Los dos catetos son iguales.
• Triángulo rectángulo escaleno: es el triángulo rectángulo que tiene todos los ángulos diferentes siempre teniendo uno de ellos de 90º. Los lados también son diferentes.

Elementos

Los elementos del triángulo rectángulo son:

• Catetos: son los lados del triángulo que juntos forman el ángulo recto.
• Hipotenusa: es el lado mayor que tiene el triángulo opuesto al ángulo recto.
• Ángulo recto: es un ángulo de 90º que se forma por los dos catetos.
• Ángulos agudos: son los otros dos ángulos del triángulo (α y β) menores de 90º. La suma de los dos ángulos agudos es de 90º.

Altura

La altura de un triángulo rectángulo se puede encontrar utilizando los siguientes teoremas:

Teorema de la altura: En cualquier triángulo rectángulo la altura relativa a la hipotenusa es la media geométrica que hay entre las proyecciones ortogonales de los catetos sobre la hipotenusa.

h/m = m/h

Si multiplicamos los dos miembros de la igualdad por hn entonces podemos obtener: h² = mn, por lo que h = √(mn)

Área

El área que tiene un triángulo rectángulo siempre tendrá un ángulo recto de 90°, por lo que su altura deberá de coincidir con uno de sus lados (a). El área de un triángulo rectángulo es la mitad del producto de los dos lados que forman el ángulo recto (catetos a y b). La fórmula para calcular el área del triángulo es la siguiente:

Área = ( b · a ) / 2

Siendo b la base y a el lado que coincide con la altura.

Perímetro

Conocemos como el perímetro de un triángulo rectángulo es la suma de los tres lados. Para conocerlo aplicamos una sencilla fórmula, que es la siguiente:

Perímetro = a + b + c

En donde a, b y c representan las medidas que tiene el triángulo.

Además, el triángulo rectángulo cumple también con el teorema de Pitágoras, por lo que la hipotenusa (c) se puede expresar a partir de los catetos (a y b). La fórmula para este tipo de operación es la siguiente:

Perímetro = a + b √(a²+b²)

Donde a y b son los catetos que forman el ángulo recto.

Razones trigonométricas

Los triángulos rectángulos tienen diferentes razones trigonométricas las cuales nos ayudan a saber la relación que hay entre los lados y los ángulos del triángulo. Su función principal es la de mostrarnos cuánto miden los ángulos internos del triángulo cuando conocemos las longitudes de dos lados del triángulo. Es importante recordar que los triángulos rectángulos siempre hay un ángulo de 90°. Existen tres razones trigonométricas comunes que son:

• Seno (sin): es la razón que existe entre el cateto opuesto y la hipotenusa y cada uno de ellos le corresponde un ángulo.
• Coseno (cos): es el resultado que se da al dividir el lado adyacente entre la hipotenusa.
• Tangente (tan): resultado de dividir las longitudes de los lados opuestos y adyacentes al ángulo α.

Por lo tanto, tenemos que:

• Lado Opuesto / Hipotenusa = Seno del ángulo
• Lado Adyacente / Hipotenusa = Coseno del ángulo
• Lado Opuesto / Lado Adyacente = Tangente del ángulo

Cómo calcular el ángulo de un triángulo rectángulo

Las alturas de los triángulos rectángulos se encuentran asociadas a los catetos (a y b). Por lo tanto, ha=b y hb=a. La altura asociada a la hipotenusa se conoce como hc. Las tres alturas del triángulo convergen en el ortocentro, H en el vértice C del ángulo recto.

Para poder calcular la altura asociada al lado c (la hipotenusa) se recurre al teorema de la altura.

La altura h puede obtenerse conociendo los tres lados del triángulo rectángulo y se aplica la siguiente fórmula:

H = ( a · b ) / c

El triángulo rectángulo posee un ángulo recto de 90°, por lo que su altura concuerda con uno de sus lados (a). Su área será entonces la mitad del producto de los dos lados que forman el ángulo recto (catetos a y b). Se utiliza la siguiente fórmula:

Área = ( b · a ) / 2

Ejemplos

Algunos ejemplos de cómo solucionar las áreas de los triángulos rectángulos son los siguientes:

Sea un triángulo rectángulo con los lados que forman el ángulo recto (a y b) conocidos, siendo a=3 cm y b=4 cm. ¿Cuál es su área?

Aplicamos la fórmula anterior del área de un triángulo rectángulo ( b · a ) / 2 y se obtiene que su área es de 6 cm².

El área de un triángulo rectángulo se puede obtener a partir de la hipotenusa y la altura del triángulo asociada a esta mediante el teorema de la altura.

Sean n y m las proyecciones de los catetos (b y a). Entonces el área de un triángulo rectángulo viene definida por la siguiente fórmula:

Área = ( c · √( n·m)) / 2

Fórmula del área de un triángulo rectángulo por el teorema de la altura. Este método es útil si no se conocen los catetos (a y b).