Trigonometría

La matemática es un área sumamente extensa y se encuentra dividida en varias ramas que estudian aspectos determinados y afines con la misma. Una de estas ramas se conoce con el nombre de trigonometría la cual se encuentra estrechamente relacionada con las funciones específicas que tienen los ángulos.

Temas relacionados

Geometría, álgebra, geometría plana, álgebra lineal

¿Qué es la trigonometría?

De la trigonometría es una rama de la matemática que se encarga de estudiar los diferentes tipos de razones trigonométricas que incluyen seno, coseno, tangente, cotangente, secante y cosecante interviniendo de forma directa o indirecta en todas las demás ramas matemáticas.

Definición

La trigonometría es una rama de la matemática que se encarga de estudiar las razones trigonométricas y las esferas dentro de la geometría espacial. Puede ser definida como la responsable de calcular todos los elementos que forman parte de los triángulos por medio del estudio de las relaciones que existen entre los ángulos y los lados de los mismos.

Características de la trigonometría

Entre las principales características de la trigonometría encontramos las siguientes:

• Es una ciencia que estudia los ángulos de los triángulos.
• Resulta ser necesaria para lograr encontrar medidas relacionadas con la precisión.
• La palabra trigonometría proviene del griego “trigonos” que tiene somo significado triángulo y de la palabra “metros” que significa medición.
• Interviene de forma directa o indirecta en otras ramas de la matemática.
• Utiliza una serie de unidades angulares que se encargan de medir los ángulos las cuales son el grado sexagesimal, el radian y el sistema decimal.

Antecedentes

Los antecedentes de la trigonometría se remontan a la época del antiguo Egipto y Babilonia, ya para ese momento existía un relativo conocimiento con respecto a las diferentes proporciones que tenían los triángulos. Estas civilizaciones se enfocaban principalmente en el estudio de los cuerpos celestes y para lograr determinar el movimiento de los planetas utilizaban un tipo de tabla de secante. Además, los egipcios fueron los constructores de las pirámides las cuales son consideradas como un tipo de trigonometría primitiva.

Historia

La historia de la trigonometría inicia en Babilonia y Egipto lugares en donde se establecieron por primera vez las aproximaciones de medidas de ángulos y longitudes para los lados de los triángulos rectángulos. Esta ciencia era muy utilizada en el campo de la astronomía, agricultura y en la construcción de pirámides. Luego, la trigonometría llegó a Grecia en donde Hiparco de Nicea logró desarrollarla aún más y construyó una tabla de cuerdas con el objetivo de poder solucionar y encontrar los ángulos de los triángulos. Tolomeo también formó parte importante de la historia trigonometría resultó fundamental para los astrónomos.

De la misma manera, la ciencia cobró importancia en lugares como India y Arabia en donde se desarrollaron sistemas trigonométricos basados en la función seno sustituyendo las cuerdas que habían sido creadas por los griegos. En el siglo XII, en Europa, empiezan a aparecer trabajos relacionados con la materia, uno de los más importantes escritos por el astrónomo y matemático Johann Müller. A inicio del siglo XVII, John Napier logra descubrir los logaritmos llamados “números artificiales” los cuales pasarían a ser un aspecto trascendental en el desarrollo de la trigonometría.

En el siglo XVII, Isaac Newton logra descubrir el cálculo diferencial e integral y en el siglo XVIII, Leonhard Euler, explica que las propiedades de la trigonometría eran una consecuencia directa que provenía de la aritmética de números complejos. Realizó varios estudios con respecto a las funciones trigonométricas y es a él a quien se le atribuye el descubrimiento de la letra e como la base del logaritmo natural. En el siglo XX, la trigonometría logró avanzar de forma importante y se empezó a utilizar en muchas Ciencias modernas.

Para qué sirve la trigonometría

La trigonometría tiene un papel importante en varias áreas que están relacionadas con las matemáticas y sobre todo en aquellas en las que la precisión resulta ser un aspecto fundamental. Con ella es posible realizar mediciones de distancias entre dos diferentes ubicaciones por medio de técnicas de triangulación y por esta razón es muy utilizada en los sistemas de navegación satelital. Es también aplica en el campo de la geometría y la astronomía y para realizar mediciones de distancias entre diferentes puntos geográficos.

Elementos

Los elementos de la trigonometría son los siguientes:

• Medición de los ángulos: los ángulos deben de medirse con sistema sexagesimal es y centesimales para lograr obtener la medida del sistema circular.
• Sistema centesimal: este sistema es definido como la 100ª parte de un ángulo recto.
• Sistema circular: utiliza la medida conocida con el nombre de radian el cuál es la longitud del arco (s) igual al radio (r).
• Equivalencias entre los sistemas de medidas.
• Circunferencia trigonométrica o unitaria: herramienta que sirve para poder visualizar y definir las razones trigonométricas de cualquier ángulo.
• Relaciones trigonométricas.

Funciones

La función trigonométrica ha sido establecida con el objetivo de poder extender la definición relacionada con las razones trigonométricas que forman parte de los números reales y complejos. Tienen una especial importancia en el campo de la astronomía, física, cartografía y las telecomunicaciones entre otras. Son definidas como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos.

Existen además 6 diferentes funciones trigonométricas básicas las cuales son:

• Seno: su abreviatura es sen o sin. Es la razón que existe entre el cateto opuesto al ángulo y la hipotenusa.
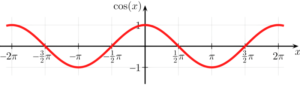
• Coseno: la abreviatura de coseno es cos. Es una función par continua y además trascendente. Es definido como la razón que existe entre el cateto adyacente al ángulo y la hipotenusa.
• Tangente: la tangente tiene como abreviatura las siglas tan o tg. Es un tipo de función impar. Es definida como la razón que existe entre el cateto opuesto y el adyacente.
• Cotangente: la cotangente utiliza las siglas ctg o cot. Es una razón trigonométrica inversa a la tangente.
• Secante: la sigla de la secante es sec. Es una función recíproca al coseno y es al mismo tiempo su inverso multiplicativo.
• Cosecante: la cosecante tiene como siglas csc o cosec. Es una razón trigonométrica recíproca del seno.

Identidades

Una identidad trigonométrica es un tipo de igualdad que tiene la función vincular de dos funciones trigonométricas. Se encuentran unidas por medio de operaciones racionales potencias de exponentes enteros.

Estas identidades se mencionan a continuación:

• Relación entre seno y coseno.
• Relación entre secante y tangente.
• Relación entre cosecante y cotangente.
• Funciones trigonométricas recíprocas.

Importancia de la trigonometría

La trigonometría es una de las ciencias más importantes para toda la humanidad porque gracias a ella se pueden realizar una serie de cálculos sobre superficies y distancias. Es una ciencia que es utilizada todos los días para realizar actividades cotidianas pues básicamente todo lo que nos rodea necesitará ser medido en algún momento determinado.

Ejemplos

Un ejemplo se muestra a continuación:

Calcular el seno, el coseno y la tangente de los ángulos α y β del siguiente triángulo:

Ángulo α:

Ángulo β: