Valor absoluto

En el terreno de las matemáticas existen muchos términos importantes, entre ellos podemos encontrar el valor absoluto el cual es utilizado con el objetivo de poder nombrar el valor que posee una determinada cifra más allá de su signo. Es conocido también con el nombre de módulo.

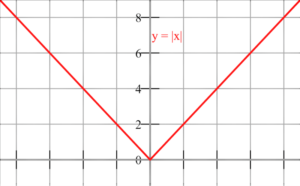
Función

f(x) = |x|

¿Qué es el valor absoluto?

El valor absoluto de un número real sin importar cuál sea es el mismo número pero con la diferencia que éste siempre deberá de tener un signo positivo. Es un valor numérico que no toma en cuenta su signo, positivo o negativo.

Definición de valor absoluto

Básicamente podemos decir que el valor absoluto de un número se refiere al valor que éste tenga sin importar el signo. A pesar de que en el campo del álgebra el tamaño, el valor y el signo importan, existen algunos casos en las matemáticas y la vida diaria en las que ese signo no es de importancia sino que lo que realmente importa es el tamaño, éste es el valor absoluto de un número.

En su definición, el concepto nos indica en otras palabras que el valor absoluto que tiene un determinado número siempre será igual o mayor que 0 pero que nunca podrá ser negativo. En este caso es importante mencionar que debido a esto, el valor absoluto que tienen los números, por ejemplo, 4 y -4 siempre será |4|.

Cuando se encuentra en una recta numérica, el valor absoluto se representa como la distancia que se da desde un determinado punto de origen. En otras palabras, si se recorren siete unidades a partir del cero hacia el lado izquierdo o hacia el lado derecho, estaremos llegando en la recta al número 7 o -7, por lo que el valor absoluto de estos valores siempre será de 7.

Un aspecto importante del valor absoluto es que éste se representa por medio de dos barras conocidas como barras de valor absoluto. Es muy importante que cuando se trabaje con él, no se confundan estas barras por paréntesis o corchetes pues en matemáticas, esto podría cambiar todas las reglas e incluso las definiciones.

Función

La principal función que tiene el valor absoluto es la de poder representar la distancia que existe desde el origen o desde el cero de un número en una recta numérica hasta llegar al número o punto de destino. Esta distancia siempre será positiva o nula.

La función del valor absoluto cuenta con su propia ecuación la cual es:

f(x) = |x|

Esta función, se representa por medio de distancias o intervalos los cuales son conocidos con el nombre de trozos o tramos y éstos pueden ser calculados si se siguen los pasos siguientes:

• Se igualará a cero la función, sin tomar el valor absoluto y luego se calculas las raíces o los valores de x.
• Se crean intervalos con las raíces de los valores de x y luego se evalúa el signo de cada uno de estos intervalos.
• La función se define entonces en intervalos teniendo siempre en cuenta que cuando la x es negativa, el signo de la función se cambia.

Propiedades del valor absoluto

Entre las principales propiedades que podemos encontrar en el valor absoluto de un número se mencionan las siguientes:

• El valor absoluto puede llegar a ser explorado de forma gráfica o de forma numérica.
• Siempre será positivo o cero. En ese aspecto es importante recordar que si el valor original del número es positivo o cero, entonces el valor siempre será el mismo. Cuando es negativo, solo se debe eliminar el signo.

También podemos encontrar varias propiedades fundamentales que son las siguientes:

• Propiedad multiplicativa: |x∙y| = |x|∙|y|
• Definición positiva: |x| = 0 ↔ x = 0
• No tiene negatividad: |x| > 0
• Pose desigualdad triangular: |x + y| ≤ |x| + |y|
• Tiene simetría: |-x| = |x|
• Es equivalente a la propiedad de la suma: |a – b| ≥ |(|a| – |b|)|
• Cuenta con identidad de indiscernibles: |a – b| = 0 ↔ a = b
• Preservación de la división, la cual es también equivalente a la propiedad multiplicativa: |x ÷ y|= |x| ÷ |y| si b ≠ 0

Símbolo

El símbolo que se utiliza para representar el valor absoluto es una barra que se coloca a cada uno de los lados del número. En lugar de decimos “el valor absoluto de 3” podemos representarlo de la siguiente manera:

∣3∣

En qué se diferencia del valor relativo

Es importante mencionar que todos los números cuentan con un valor absoluto y un valor relativo. La principal diferencia es que el valor absoluto es aquel que hace referencia específicamente al valor numérico y no toma en cuenta nada de lo que se pueda encontrar antes o después del número, por ejemplo, el valor absoluto de 5 y -5 siempre será 5.

Por otra parte, el valor relativo puede ser encontrado tomando en cuenta el valor que tienen los números que conforman una cifra, en otras palabras, si tenemos por ejemplo el número 589, cada uno de estos números tendrá su propio valor relativo tomando en cuenta también su posición. El 9 será nueve pues está en la posición de las unidades, el 8 tendrá un valor de 80 por estar en el lugar de las centenas mientras que el 5 tendrá un valor de 500 pues se encuentra en el lugar de las centenas.

Importancia

Su importancia radica en el momento de realizar diferentes cálculos que deben de ser positivos pues para ello se debe tomar primeramente el valor menor. Además es un término que está muy relacionado con términos como la magnitud, la distancia y la norma en un amplio campo de contextos matemáticos y físicos.

Ejemplos de valor absoluto

Algunos ejemplos de valor absoluto se mencionan a continuación:

• (6) = 6, porque 6 > O
• (-9) = (-9) porque -9 < O tomamos su inverso
• Si (x) = 5 entonces x = 5 o x= -5